| Indietro | ||
Procedure di ricerca locale per la soddisfacibilità booleana
Le
performance di una procedura di ricerca locale stocastica dipendono
dall’impostazione del parametro di noise,
che determina
la probabilità di uscire dai minimi locali facendo mosse non ottimali. Nel
simulated annealing [82], [23], questa è la temperatura;
nella ricerca tabu [51], [52], il periodo
di possesso -
la durata di tempo per il quale una variabile modificata è tabu; nel GSAT [113] - il parametro random
walk, e nel
WSAT anche chiamata walksat, [114] - il parametro è stato semplicemente chiamato noise.
L'impostazione ottimale del parametro noise dipende dalle caratteristiche delle
istanze del problema, e dai dettagli strutturali della procedura di ricerca che
potrebbe essere influenzata da altri parametri. Si richiede uno sforzo
considerevole per trovare il parametro noise ottimale che mette per una data
distribuzione di problemi usando trialanderror. Inoltre, qualche volta si
affronta un problema unico, difficile da risolvere, e perciò non si può
regolare il noise risolvendo altri problemi simili.
Così
sarebbe desiderabile di trovare un modo per impostare il parametro noise che non
varia con particolari algoritmi di ricerca o istanze di problemi particolari.
McAllester
e al. hanno studiato sei variazioni dell’architettura del WSAT di base su una
classe di istanze di problemi random difficili. Secondo questo studio hanno
scoperto due invariants.
Primo,
per una data classe di problemi, il livello di noise misurato dal valore
della funzione obiettivo (il numero di clausole non soddisfatte)
all’impostazione del parametro ottimale è stato approssimativamente costante
attraverso le strategie. McAllester e al. hanno chiamato questo invariante
del livello di noise.
Hanno scoperto addirittura un principio più generale, che mostra che
l'impostazione del parametro ottimale minimizza approssimativamente il rapporto
della media della funzione obiettivo alla sua varianza. Hanno mostrato come
questo invariante dell’ottimalità può essere utilizzato per impostare il parametro noise
per un’unica istanza del problema, senza avere prima risolto quell'istanza od
una simile. Come vedremo, il valore ottimale del parametro noise, per una
strategia data, può essere estimato rapidamente e accuratamente analizzando le
proprietà statistiche di molte esecuzioni corte della strategia.
Per
verificare che questi invarianti non sono dovuti semplicemente alle proprietà
speciali delle istanze random, poi McAllester e al. hanno confermato le loro
scoperte su istanze estremamente strutturate dai domini di pianificazione e
Graph Coloring.
I
risultati presentati provvedono immediati orientamenti pratici per
l'impostazione dei parametri per il WSAT e le sue versioni. McAllester e al.
hanno ulteriormente ipotizzato che gli stessi invarianti si mantengono
attraverso altre classi di procedure di ricerca locale, perché le versioni di
WSAT che avevano considerato erano infatti basate su alcune di queste procedure.
Lo stato attuale della teoria della ricerca locale non permette di dedurre
analiticamente l’esistenza di questi invarianti.
Un'altra
conseguenza pratica del lavoro di McAllester e al., è che può essere
utilizzato per aiutare alla progettazione di nuove euristiche per la ricerca
locale. Siccome le euristiche locali sono così sensibili all’impostazione del
loro parametro noise, un’euristica si può solamente escludere se è esaminata
alla sua calibrazione ottimale. Quando si verificano dozzine o centinaio di
euristiche, comunque è proibitivo computazionalmente esaminare esaurientemente
ogni parametro dell’impostazione. Comunque, nella ricerca delle euristiche
migliori, l’impostazione dei parametri determinati dagli invarianti hanno
prodotto costantemente le migliori performance per ogni strategia. Questo ha
permesso a McAllester e al. di identificare rapidamente due nuove euristiche che
migliorano rispetto a tutte le altre variazioni del WSAT sulle istanze di prova.
Certamente,
ci sono stati precedenti studi comparativi sulle performance dei diversi
algoritmi di ricerca locale per il SAT. Per esempio, Gent e Walsh [36] hanno comparato le performance di alcune versioni del GSAT,
concludendo che l’HSAT potrebbe risolvere più rapidamente i problemi random.
Qui lo scopo è diverso: McAllester e al. sono meno interessati nel trovare il
migliore algoritmo per le istanze random che nel trovare principi generali che
rivelano se algoritmi differenti stanno percorrendo nella stessa maniera o no lo
stesso spazio di ricerca. Parkes e Walser [105] hanno studiato una versione modificata del WSAT, mentre usando la
funzione di minimizzazione del GSAT con il livello di noise impostato a
p = 50%.
Loro conclusero che il WSAT originale era superiore alla versione modificata.
Come vedremo, comunque, il parametro p ha valori ottimali diversi per strategie diverse, ed in
particolare non è ottimale a 50%
per il WSAT modificato. Un recente lavoro di Battiti e Protasi [3] è abbastanza simile allo studio presente, loro sviluppano uno
schema di reazione per calibrare i parametri di noise degli algoritmi di ricerca
locale SAT. Il loro calcolo è basato sulla distanza media di Hamming.
Consideriamo
gli algoritmi per risolvere i problemi di soddisfacibilità booleana in CNF. Nel
3SAT,
ogni clausola contiene esattamente tre letterali distinti. Le clausole nella
formula 3SAT random sono generate scegliendo a caso tre letterali
distinti, e poi negando o no ognuno con uguale probabilità. Mitchell et al. [98] hanno mostrato che i problemi 3SAT random sono computazionalmente difficili, quando il
rapporto tra clausole a variabili in tale formula è approssimativamente uguale
a 4.3.
Una
procedura di ricerca locale si muove in uno spazio di ricerca dove ogni punto è
un assegnamento di verità delle variabili date. La procedura WSAT comincia
considerando un assegnamento di verità random. Cerca una soluzione selezionando
a caso ripetutamente una clausola violata, e poi utilizzando alcune euristiche
per selezionare una variabile da modificare (flip - la modifica da True
a False
o viceversa) in quella clausola.
La
funzione obiettivo della ricerca locale per SAT tenta minimizzare il numero
totale di clausole non soddisfatte. La caratteristica della strategia di ricerca
che la induce a fare mosse che sono non ottimali - nel senso che le mosse
aumentano o non riescono far decrescere la funzione obiettivo, anche quando sono
disponibili tali mosse migliorativi nel vicinato locale dello stato corrente -
è chiamato noise.
Come notato prima, il noise permette alla procedura di ricerca locale di uscire
dall'ottimo locale.
Ogni
euristica descritta sotto prende un parametro che può variare la quantità del
noise nella ricerca. Come vedremo, i valori presunti da questo parametro non
sono direttamente comparabili attraverso le strategie: per esempio, un valore di
0.4
per una strategia può produrre una ricerca con mosse frequentemente non
migliorative, della ricerca compiuta da una strategia diversa con lo stesso
valore del parametro.
McAllester
e al. hanno considerato sei euristiche per selezionare una variabile all'interno
di una clausola. Le prime quattro sono variazioni delle procedure conosciute,
mentre le ultime due sono nuove. Loro sono:
·
G -
con probabilità p scelgo qualsiasi variabile, altrimenti scelgo un
variabile che minimizza il numero totale di clausole non soddisfatte. Il valore
p
è il parametro noise che varia da 0 a 1.
·
B
- con probabilità p scelgo qualsiasi variabile, altrimenti scelgo una
variabile che minimizza il numero di clausole che sono True
nello stato corrente, ma che diventerebbe False
se il cambio sarebbe fatto. Nella descrizione originale del WSAT, questa è
stata chiamata minimizing
breaks. Di
nuovo p è il parametro noise.
·
SKC
- come la precedente, ma non fa mai una mossa random se esiste una con breakvalue
di 0.
Notiamo che quando il breakvalue è 0,
allora la mossa è garantita a migliorare anche la funzione obiettivo. Questo è
il WSAT originale proposto da Selman, Kautz e Cohen (1994).
·
TABU
- la strategia è di scegliere una variabile che minimizza il numero delle
clausole non soddisfatte. Comunque, ad ogni passo rifiuta modificare qualsiasi
variabile che è stata modificata negli ultimi t
passi; se
tutte le variabili delle clausole non soddisfatte sono tabu, sceglie invece una
clausola diversa non soddisfatta. Se tutte le variabili in tutte le clausole non
soddisfatte sono tabu, allora la lista tabu è ignorata. La lista tabu di
lunghezza t
è il
parametro noise.
·
NOVELTY
- questa strategia ordina le variabili in base al numero totale di clausole non
soddisfatte, come fa G,
ma rompendo il collegamento in favore della variabile modificata più
recentemente. Consideriamo la migliore e la seconda migliore variabile sotto
questo criterio. Se la migliore variabile non è la variabile più recentemente
modificata nella clausola, la selezioniamo. Altrimenti, con probabilità
p selezioniamo la seconda migliore variabile, e con
probabilità 1
– p la
migliore variabile.
·
R_NOVELTY
- questo è lo stesso come NOVELTY, eccetto il caso quando la migliore variabile
è la più recentemente modificata. In questo caso, sia n
la differenza della funzione obiettivo tra la migliore e la seconda migliore
variabile. Notiamo che n
³ 1. Ci sono poi quattro casi:
1.
Quando p
< 0.5
e n >
1, scelgo
alla migliore
2.
Quando p
< 0.5 e n = 1, allora con probabilità
2p scelgo la seconda migliore, altrimenti scelgo la
migliore.
3.
Quando p
³
0.5
e n = 1, scelgo la seconda migliore
4.
Quando p
³
0.5 e
n >
1, allora con
probabilità 2
( p – 0.5 )
scelgo la seconda migliore variabile, altrimenti la migliore.
L’intuizione
dietro il NOVELTY e che si vuole modificare ripetutamente la stessa variabile
indietro e in avanti. L’intuizione dietro il R_NOVELTY e che la funzione
obiettivo dovrebbe influenzare la scelta tra la migliore e la seconda migliore
variabile - una grande differenza della funzione obiettivo favorisce la
migliore. Notiamo che la R_NOVELTY è quasi deterministico. Per rompere i loop
deterministici nella ricerca, ogni 100
flips la
strategia seleziona una variabile random dalla clausola. Anche se pochi flips
comportino non determinismo, vedremo che le performance del R_NOVELTY sono
ancora abbastanza sensibili all’impostazione del parametro
p.
Il
noise nella ricerca locale può essere controllato da un parametro che specifica
la probabilità di una mossa locale non ottimale, come nelle strategie G, B e
SKC, NOVELTY, e R_NOVELTY. Invece le procedure tabu prendono un parametro che
specifica la lunghezza della lista tabu. Le ricerche con liste tabu corte sono
più suscettibili ai minimi locali (sono meno rumorose) delle ricerche con liste
tabu lunghe.
Nella
Figura 9.1 sono mostrati i risultati di una serie di esecuzioni delle diverse
strategie come una funzione dell’impostazione del parametro noise, su una
collezione di 400
istanze 3SAT random difficili. Sull’orizzontale è rappresentata
la probabilità di una mossa random. La lunghezza del tabu varia da 0 a 20,
è stata normalizzato nel grafico alla serie 0
- 100. L'asse
verticale specifica la percentuale delle istanze risolte. Ogni punto di dati
rappresenta 16.000
esecuzioni con una formula diversa per ognuna, dove il numero massimo di flips
per esecuzione è fissato a 10.000.

Figura 9.1: Le sensitività al noise
Sono stati
rappresentati il valore del parametro noise rispetto alla frazione delle istanze
che sono state risolte. Per esempio, R_NOVELTY ha risolto quasi 16% delle istanze del problema quando
p
è stato impostato su 60%. Considerando la frazione risolta con un numero fisso di
flips ha permesso di raccogliere statistiche accurate sull'efficacia di ogni
strategia. Se invece si tentava di risolvere ogni istanza, si affrontava il
problema di trattare con la variazione alta nel run-time delle procedure
stocastiche - per esempio, alcune esecuzioni potrebbero richiedere millioni di
flips - ed il problema di trattare con esecuzioni che non convergono mai.
Come è chiaro dalla figura, le performance di ogni strategia variano altamente, dipendendo dall’impostazione del parametro noise. Per esempio, il funzionamento di R_NOVELTY ad un livello di noise di 40% invece di 60% degrada le sue performance con più di 50%. Inoltre, le performance ottimali appaiono ad impostazioni di parametri diversi per ogni strategia. Questo suggerisce che nella comparazione delle strategie si deve ottimizzare attentamente per ogni impostazione del parametro, e che addirittura modifiche minori ad una strategia richiedono che i parametri devono essere riaggiustati in modo appropriato.
Data la precedente osservazione, sorge la domanda: esiste una caratterizzazione migliore del livello noise che è meno sensibile ai dettagli delle strategie individuali?
McAllester e al. hanno esaminato un numero di misure diverse del comportamento delle strategie di ricerca locale. Definiamo il livello noise normalizzato di una procedura di ricerca su un’istanza del problema dato come il valore medio della funzione obiettivo durante un’esecuzione di quell’istanza. Allora, si può osservare che il livello noise normalizzato ottimale è approssimativamente costante attraverso le strategie. Questo è illustrato nella Figura 9.2.

Figura 9.2: Invariante del livello di noise normalizzato nelle formule random
In altre parole, quando il parametro noise è ottimamente calibrato per ogni strategia, allora il numero medio delle clausole non soddisfatte durante un’esecuzione è approssimativamente lo stesso attraverso le strategie.
Chiamiamo questo
fenomeno invariante del livello di noise,
che rappresenta un attrezzo utile per la progettazione e per calibrare i metodi
di ricerca locale. Una volta McAllester e al. hanno determinato il conteggio
medio delle violazioni dando le performance ottimali per una singola strategia
su una distribuzione data di problemi, hanno potuto semplicemente calibrare le
strategie altre per funzionare allo stesso conteggio medio delle violazioni,
nella conoscenza che questo ci darà vicino alle performance ottimali.
Dopo
aver ipotizzato l'esistenza di questo invariante, McAllester e al. hanno voluto
verificare anche per le classi del mondo reale, problemi strutturati di
soddisfacibilità. Le Figure 9.3 e 9.4 presentano la conferma di
quest’evidenza.

Figura 9.3: Invariante del livello di noise normalizzato nelle formule di pianificazione
La Figura 9.3 è
basata sulla risoluzione di un problema di soddisfacibilità che codifica un
problema di pianificazione blocksworld, l'istanza bw_large.a
da Kautz e Selman [78]. Il problema originale è di trovare un piano 6step che risolve
un problema di pianificazione che comporta 9 blocchi, dove ogni passo nuove un blocco. Dopo il
problema è codificato e semplificato dall’unit propagation, contiene 459 variabili e 4675
clausole. Ogni procedura stocastica è stata eseguita 16.000
volte. Notiamo che questo è diverso del caso con le formule random, dove è
stata generata una formula diversa per ogni prova.

Figura
9
.4: Invariante del livello di noise normalizzato nelle formule di graph
coloring
Figura
9.4 mostra l’invariante del livello di noise su una codifica SAT di un
problema di Graph Coloring. L'istanza è basata su 18
colori di 125 nodi di un grafo (Johnson e al. [70]). Questa formula contiene 2.250 variabili e 70.163
clausole. Siccome questa formula è così grande, McAllester e al. non hanno
potuto compiere molte esecuzioni come nei precedenti esperimenti. Ogni punto è
basato su appena 1.000 campioni,
e questo spiega la natura piuttosto irregolare delle curve.
L’invariante del livello di noise non implica che tutte le strategie sono equivalenti in termini del loro livello di performance ottimali.
McAllester
e al. hanno sperimentato con un gran numero di euristiche per selezionare la
variabile da cambiare nel WSAT per risolvere i problemi di soddisfacibilità
booleana. L’invariante del livello di noise ha permesso di valutare
rapidamente più di 50
versioni del
WSAT, e ognuna è stato esaminata con il suo livello di noise ottimale. Questo
ha portato allo sviluppo delle strategie NOVELTY e R_NOVELTY che costantemente
migliorano quasi due volte rispetto alle altre versioni.
L’invariante del livello di noise dà delle possibilità di trattare con la sensività del noise delle procedure di ricerca locale. Comunque per usarlo si ha bisogno di essere capaci di raccogliere delle statistiche sulla rata di successo di almeno una strategia attraverso un esemplare di una distribuzione di problemi. In pratica McAllester e al. hanno affrontato spesso la necessità di risolvere una particolare istanza di un nuovo problema. Inoltre, quest’istanza può essere estremamente difficile, e risolverla può richiedere una grande quantità di calcolo anche all’impostazione del noise ottimale. Perciò, si desidera di predire rapidamente l’impostazione del parametro di noise per una singola istanza del problema, senza doverla risolvere.
Lo
studio empirico della sensività del noise, ha prodotto un principio preliminare
per impostare i parametri di noise in base alle proprietà statistiche della ricerca. McAllester e al. hanno eseguito molte
esecuzioni corte della procedura di ricerca, e hanno registrato il valore finale
della funzione obiettivo per ogni esecuzione e la variazione dei valori su
quell’esecuzione. Poi, hanno preso la media di questi valori.
Per
illustrare il principio, McAllester e al. hanno presentato nella Figura 9.5 i
problemi risolti come una funzione del rapporto tra il valore medio e la
variazione su una collezione di istanze di problemi random difficili. Per ogni
strategia i dati puntano a formare un loop.

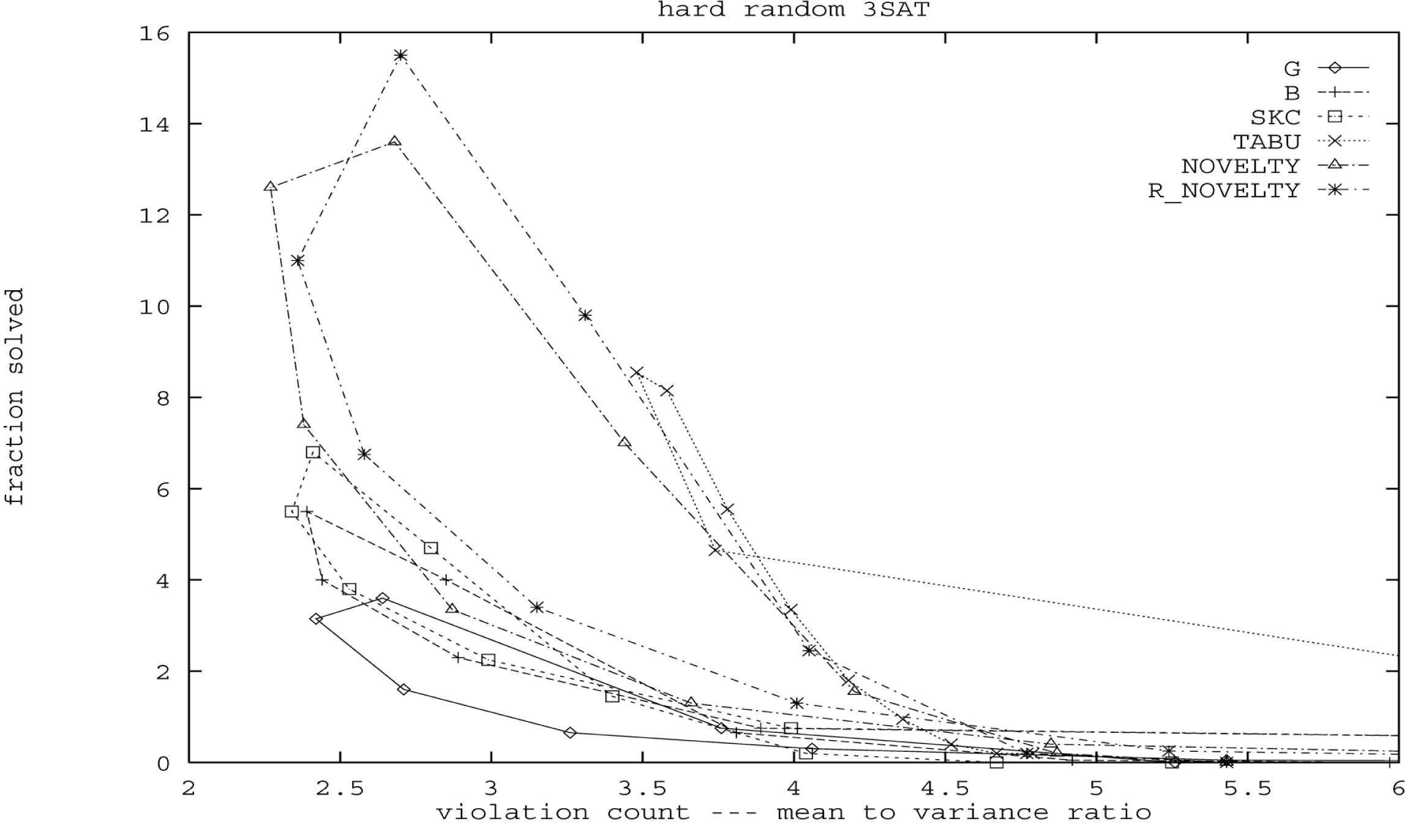
Figura 9.5: Tuning noise sulle istanze random
Traversando
il loop in una direzione destrorsa che comincia dall'angolo basso in destra
corrisponde a incrementare il livello di noise da 0 al suo valore massimo. Nello stesso punto durante questo
attraversamento si raggiunge un valore minimo del rapporto tra il valore medio e
la variazione. Per esempio, la strategia R_NOVELTY (la curva più alta) ha un
minimo del rapporto tra il valore medio e la variazione intorno a 2.5. A quel punto risolve approssimativamente 11% delle istanze. Alzando il noise, e aumentando di nuovo
il rapporto tra il valore medio e la variazione, giungiamo alle performance di
picco di 15%
ad un rapporto di 2.8. Si osserva lo stesso modello per tutte le strategie.
Nei loro esperimenti McAllester e al. hanno trovato le performance ottimali
quando il rapporto è approssimativamente 10%
più alto del suo valore minimo.
Le Figure 9.6 e 9.7
confermano di nuovo questa osservazione sulle istanze di pianificazione e Graph
Coloring. Di nuovo si vede che tutte le curve raggiungono leggermente il loro
picco alla destra del rapporto tra il valore medio e la variazione.
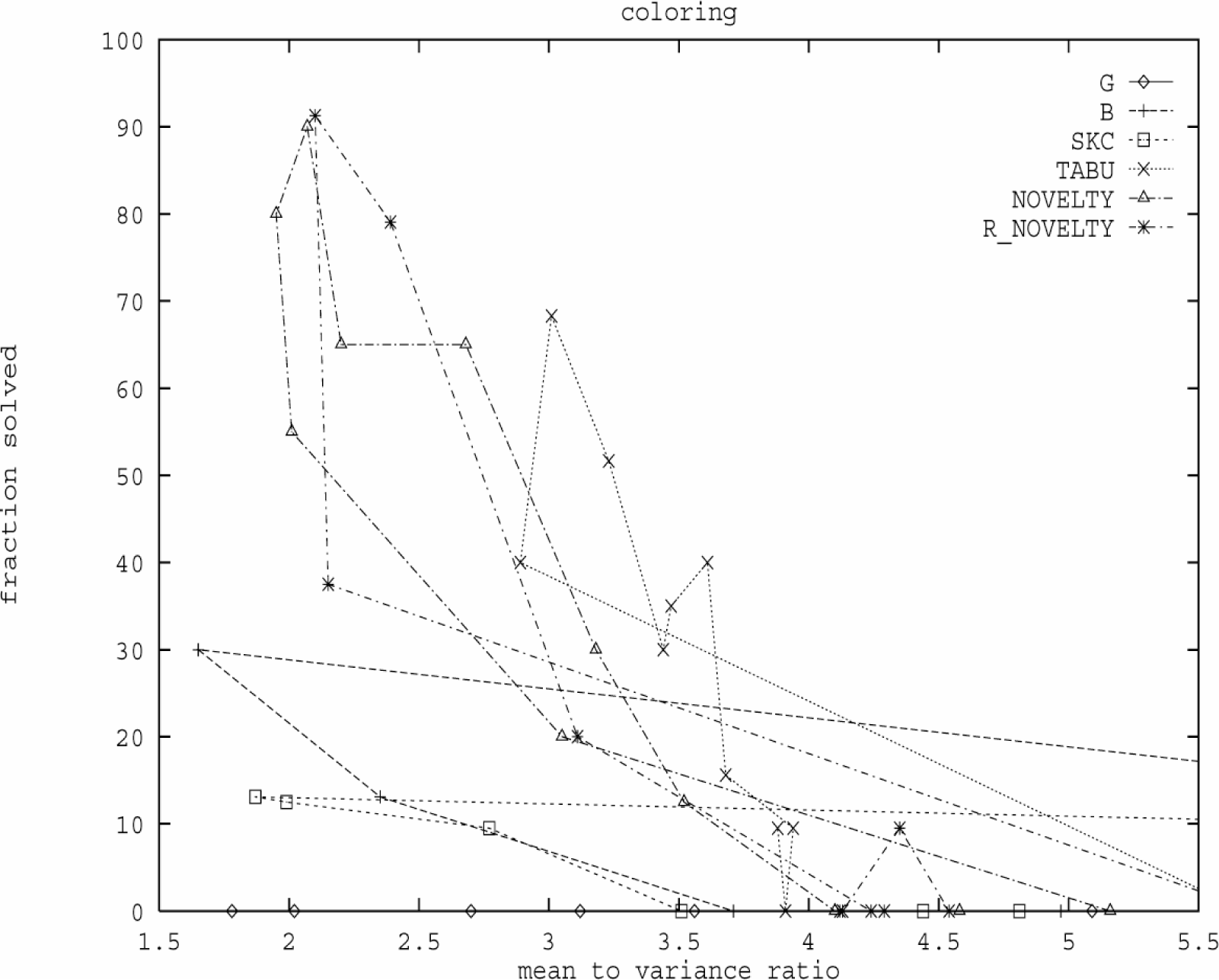
Figura 9.6: Tuning noise sulle istanze di pianificazione

Figura 9.7: Tuning noise sulle istanze di coloring
McAllester
e al. hanno sottolineato di nuovo che misurando il rapporto tra il valore medio
e la variazione non richiede la risoluzione dell'istanza del problema. Per ogni
valore di noise, hanno potuto misurare il rapporto facendo semplicemente molte
esecuzioni corte e hanno calcolato il valore medio e la variazione del conteggio
delle violazioni durante l’esecuzione. Poi, ripetendo questa procedura per
impostazioni diverse del parametro di noise, sono riusciti a determinare le
impostazioni necessarie per ottenere il rapporto tra il valore medio e la
variazione che è 10%
sopra il suo minimo.
Un
altro modo di risolvere un'istanza di un unico problema è avviare
l’esecuzione ad un livello di noise arbitrario. Poi si può misurare il
rapporto tra il valore medio e la variazione durante l’esecuzione, e
aggiustare dinamicamente il livello di noise per ottenere le performance
ottimali.
| Indietro | ||
| Satz |
SAT solver |
Conclusioni |