| Indietro | ||
Miglioramenti resovent-driven del Satz
Risultati comparativi sperimentali sui problemi 3SAT difficili
Risultati comparativi sperimentali dei problemi SAT strutturati
Chu Min Li ed Anbulagan propongono una
procedura DPL molto semplice chiamata Satz che assume solamente alcune tecniche
look-ahead: un’euristica con ordinamento di variabili, un controllo di
consistenza in avanti FCC (Unit propagation) e una risoluzione limitata prima
della ricerca, dove l'euristica è se stessa basata su unit propagation. Satz è
comparata sui problemi 3SAT random con tre procedure di DPL fra le migliori
nella letteratura per questi tipi di problemi. Inoltre, su un grande numero di
problemi in 4
ben
conosciuti benchmark SAT, Satz raggiunge o addirittura supera le performance
delle altre tre procedure DPL per i problemi SAT strutturati. I risultati
comparativi suggeriscono che un utilizzo appropriato della tecnica look-ahead può
permettere di fare a meno nella procedura DPL delle sofisticate tecniche
look-back.
Consideriamo
un set di variabili booleane {x1,x2,…,xn}. Per le definizioni del letterale, clausole, formule
proposizionali e soddisfacibilità
vedi [1.5.1], [1.5.2], [1.5.3].
Distinguiamo due tipi di problemi SAT:
·
problemi
che hanno strutture come regolarità, simmetrie;
·
problemi
random senza alcuna struttura.
Mentre
i problemi del mondo reale sono spesso strutturati, i problemi random
rappresentano il core del SAT e sono indipendenti da qualsiasi dominio
particolare.
I
più efficaci algoritmi sistematici sono basati sulla procedura ben conosciuta
di Davis-Putnam nella forma di Loveland - procedura DPL [19]. Procedure DPL come CSAT [22], Tableau [16], e POSIT [26] di solito utilizzano un’euristica con ordinamento di variabili, e
un FCC noto come tecnica look-ahead in termini di CSP. Questi algoritmi
attualmente hanno in parte difficoltà nel risolvere problemi SAT strutturati.
Recentemente molti autori hanno proposto di includere (e enfatizzare) tecnica
look-back come backjumping (noto anche come backtracking intelligente o
backtracking non cronologico) e apprendimento (noto anche come nogood) in una
procedura DPL per affrontare i problemi SAT strutturati. GRASP [117] e relsat(4) [6] sono tali procedure DPL che utilizzano le tecniche look-ahead e
look-back, che sono efficaci per i problemi SAT strutturati ma non sono efficaci
per i problemi SAT random.
Chu
Min Li and Anbulagan hanno proposto una procedura DPL molto semplice chiamata
Satz che utilizza solamente la tecnica look-ahead e un semplice pre-processing
della formula CNF per aggiungere delle soluzioni di lunghezza £
3 nel
database delle clausole. I risultati comparativi sperimentali di Satz con vari
procedure DPL (CSAT, Tableau, POSIT, GRASP, relsat(4)) suggeriscono che
l'utilizzo appropriato dell’unit propagation e il pre-processing possono essere efficaci sia per i problemi SAT random che per
quelli molto strutturati.
Tutti
gli esperimenti sono stati fatti su una workstation SUN Sparc-20 a 125 MHz.
La
procedura DPL è schematizzata nella Figura 8.1.
Essenzialmente,
la procedura DPL costruisce un albero di ricerca binaria attraverso lo spazio
degli assegnamenti di verità possibile fin quando si trova un assegnamento di
verità soddisfacente, oppure conclude che non esiste alcun assegnamento di
questo tipo, ogni chiamata ricorsiva costituendo un nodo dell'albero.

Figura
8.1
: La procedura DPL
Attualmente,
la più popolare euristica SAT è l’euristica di Mom che riguarda la
ramificazione dopo la variabile avendo le massime occorrenze nelle clausole di
dimensione minima [16], [22], [26], [65], [68], [98]. Intuitivamente, queste variabili permettono di utilizzare bene la
potenza dell’unit propagation ed aumentare l'opportunità di raggiungere una
clausola vuota.
Comunque l’euristica di Mom può anche non massimizzare l'efficacia dell’unit propagation, in quanto prende in considerazione solamente clausole di dimensione minima per pesare una variabile, anche se alcune estensioni provano a prendere in considerazione anche clausole più lunghe con pesi esponenzialmente piccoli (per esempio, cinque clausole ternarie sono contate come una clausola binaria).
Recentemente
un’altra euristica basata sull’unit propagation (euristica UP), ha
dimostrato utilità e permette di utilizzare ancora di più la potenza
dell’unit propagation [16], [26], [87], [88].
Data
un variabile x,
l’euristica UP esamina x aggiungendo rispettivamente le clausole unità x e Øx a F,
ed indipendentemente fa due unit propagation.
L’euristica UP permette poi di prendere tutte le clausole che contengono una
variabile, e le loro relazioni in accordo in un modo molto efficace per pesare
la variabile. Come un effetto secondario, permette di scoprire i così chiamati failed
literals in F, che quando soddisfatti rendono falso F in una singola unit propagation. Comunque, siccome l’esaminazione
di una variabile da parte di due unit propagation rappresenta consumo di tempo, è naturale provare a
limitare le variabili da esaminare.
Il
successo dell’euristica di Mom suggerisce che più è grande il numero delle
occorrenze binarie di una variabile, maggiore è la sua probabilità di essere
una buona variabile di ramificazione, implicando che si dovrebbe limitare
l'euristica UP a quelle variabili che hanno un numero sufficiente di occorrenze
binarie.
In
[88], Chu Min Li e Anbulagan hanno studiato
i comportamenti di diverse restrizioni dell’euristica UP sui problemi 3SAT random difficili. Loro hanno trovato che
l’euristica UP è sostanzialmente migliore di quella di Mom persino nella sua
forma pura, dove tutte le variabili libere sono esaminate in tutti i nodi.
Inoltre, più variabili sono esaminate, l'albero di ricerca è più piccolo,
confermando i vantaggi dell’euristica UP, ma troppe unit propagation
rallentano l'esecuzione.
Basandosi
su valutazioni sperimentali di vari alternative, Chu Min Li e Anbulagan
hanno avanzato una restrizione dinamica dell’euristica UP, assicurando che
almeno T variabili selezionate dall’euristica di Mom sono
esaminate dalle unit propagation. L’euristica UP risultante è realizzata dal
predicato unario PROPz.
Sia PROP un predicato binario tale che PROP(x,i) è True se x si presenta sia positivo che negativo nelle clausole binarie e avendo almeno i occorrenze binarie in F, T è un numero intero, allora PROPz(x) è definito ad essere il primo dei tre predicati PROP(x,4), PROP(x,3), True di cui la semantica denotazionale contiene più di T variabili.
PROPz
è ottimale per i problemi 3SAT random difficili. Come vedremo, è anche molto
potente per quelli strutturati.
Satz
è una procedura DPL con l’euristica UP PROPz
con T che è empiricamente fissato a 10. Sia diff(F1,F2) una funzione che da il numero di clausole di dimensione
minima in F1 ma non in F2,
la regola di ramificazione di Satz è mostrata nella Figura 8.2, dove
l'equazione H(x) è suggerita da Freeman [26
] in POSIT.

Figura
8.2
: La regola di ramificazione di Satz
Satz
permette una realizzazione molto semplice e naturale, che corrisponde
esattamente alla descrizione di sopra dell’algoritmo, eccetto il fatto che il
backtracking non è ricorsivo e la sua implementazione iterativa è inspirata
originalmente all’ULog [49
], un interprete del linguaggio Prolog. Non c'è nessun'altra tecnica
in Satz diversa dei due miglioramenti descritti nella sezione [8.3]. Per riprodurre le performance di Satz, nel programma si utilizzano
solamente degli arrays invece di strutture complesse di dati. Satz utilizza
liste collegate per alimentare le clausole, poi, prima della ricerca copia tutti
i dati negli arrays.
Hooker
e Vinay [65
] hanno studiato le ipotesi di soddisfazione e di semplificazione,
che sono spesso utilizzate per motivare o spiegare la regola di ramificazione di
una procedura DPL. A parità di condizioni, l’ipotesi di soddisfazione parte
dal presupposto che una regola di ramificazione funziona meglio quando crea
sottoproblemi che sono più probabili ad essere soddisfacibili, mentre
l’ipotesi di semplificazione parte dal presupposto che una regola di
ramificazione funziona meglio quando crea sottoproblemi con meno clausole e che
sono più corte. Una delle loro conclusioni è che l'ipotesi di semplificazione
è migliore dell’ipotesi di soddisfazione.
Satz
utilizza un'altra ipotesi chiamata ipotesi dei vincoli constraint
hypothesis che
parte dal presupposto che una regola di ramificazione funziona meglio quando
crea sottoproblemi con più vincoli e più forti, così una contraddizione può
essere trovata prima. Da quando le clausole di dimensione minima sono i vincoli
più forti in una formula di CNF, w(x)
e w(Øx) nella Figura 8.2 rappresentano rispettivamente i nuovi
vincoli dei due sottoproblemi generati se x è selezionato come la prossima variabile di
ramificazione. Secondo constraint hypothesis, la procedura DPL dovrebbe ramificare dopo x tale che w(x)
e w(Øx) sono i maggiori. L'equazione di definizione di H(x) e di collegamento w(x)
e w(Øx) in Figura 8.2 per favorire x
tale che w(x) e w(Øx) solo a grosso modo uguali e bilanciare i due sottoalberi
è sperimentalmente meglio del seguente:
w(x) +
w(Øx)+ a*min(w(x),
w(Øx))
(*)
dove
a
è una costante.
Sembra
che il CSAT utilizzi l’ipotesi di semplificazione e l'equazione (*) per
definire H(x),
mentre POSIT
prova combinare le ipotesi di semplificazione e dei vincoli, e Tableau utilizza
le ipotesi dei vincoli e la stessa equazione come POSIT per definire H(x).
CSAT
[22
] esamina una variabile vicina alle foglie di un albero di ricerca da
due unit propagation (chiamato processing locale) per scoprire rapidamente
letterali errati. Anche Pretolani ha utilizzato un approccio simile (chiamato
metodo di potatura) basato su hypergraphs in H2R [105]. Ma il processing locale ed il metodo di potatura come sono
presentati rispettivamente in [22] e [105] non contribuiscono all’euristica di ramificazione.
Troviamo
il primo utilizzo valido dell’euristica UP in POSIT [26] e Tableau [16]. POSIT e Tableau hanno un’idea simile al CSAT, per determinare
le variabili da esaminare dall’unit propagation nei nodi dell’albero di
ricerca: x
sarà esaminato dall’unit propagation se x
è fra le più pesanti k variabili.
La
differenza principale tra Satz confrontato con Tableau e POSIT, è che Satz non
specifica un limite superiore k
del numero di variabili che saranno esaminate dall’unit propagation in un
nodo. Invece, Satz specifica un confine più basso T.
Infatti, Satz esamina molte più variabili in un nodo.
Data
la profondità di un nodo, Tabella 8.1 illustra il numero medio delle variabili
libere (#free_vars)
ed il numero medio delle variabili esaminate dal Satz nel nodo (#examined_vars),
con la profondità della radice che è 0.
Per una comparazione con CSAT, Tableau e POSIT sono dati anche
i valori teoretici nel nodo di kC
(per CSAT), kT
(per Tableau) e kP
(per POSIT), rispettivamente secondo le definizioni di k
in [22], [16], [26].
Dalla
Tabella 8.1, è chiaro che Satz esamina in ogni nodo molte più variabili del CSAT,
Tableau o POSIT. Vicino alla radice, Satz esamina tutte le variabili libere.
Altrove Satz esamina un numero sufficiente di variabili.
Sempre
sotto l’ipotesi dei vincoli, Li e Ambulagan hanno fatto dei miglioramenti
resovent-driven in Satz. Il primo miglioramento è la pre-processing della
formula di ingresso aggiungendo delle soluzioni di lunghezza £
3, ispirato
da [3].

Tabella
8.1: Il numero medio di variabili esaminate da Satz per problemi 3SAT random con
300 variabili e 1275 clausole (sono stati risolti 500 problemi)
Per
esempio, se F contiene due clausole
x1Úx2Úx3; Øx1Úx2ÚØx4
allora
aggiungiamo la clausola x2Úx3ÚØx4
ad F. Le nuove clausole a turno possono essere utilizzate per
produrre altre soluzioni di lunghezza £ 3. Il processo è compiuto fino alla saturazione. In
pratica, imponiamo due vincoli:
·
una
soluzione risultata da due clausole binarie dovrebbe essere unaria per essere
aggiunta nel database della clausola,
·
una
soluzione risultata da una clausola binaria e una clausola ternaria dovrebbe
essere binaria per essere aggiunta nel database della clausola.
La
pre-processing senza i due vincoli è stabilito come una opzione.
Chiaramente,
le soluzioni aggiunte diventano vincoli espliciti in F come le altre clausole. Inoltre, una variabile vincolata
da un letterale e della sua forma negata ha una occorrenza di più per essere
vantaggiata dalla regola di ramificazione, nell'esempio di sopra questo è il
caso per x2
che è vincolato da entrambi x1
e Ø
x1.
Il pre-processing standard rende Satz approssimativamente 10% più veloce per i problemi 3SAT random difficili, e permette di risolvere istantaneamente la classe di problemi aim del benchmark DIMACS. Inoltre Satz risolve due volte più veloce i problemi della classe dubois. La pre-processing senza i due vincoli permette di risolvere istantaneamente tutti i problemi dubois.
Il
secondo miglioramento consiste nel ponderare con più precisione le variabili
nei nodi dove PROPz
è True,
per tutte le variabili, perché questi nodi sono spesso vicini alla radice
dell'albero di ricerca e la loro variabile di ramificazione ha un effetto più
importante per ridurre la dimensione dell’albero. Definiamo w(x)
come il numero di soluzioni, le nuove clausole binarie prodotte dovrebbero
risultare in F’ da un singolo passo di risoluzione. w(Øx) è definito in modo simile.
Riguardo
alla Figura 8.2, dopo avere eseguito F’=UnitPropagation(F’È{x}),
w(x) è definito:
![]() ,cond =
lÚl’
è in F’ ma non in F
,cond =
lÚl’
è in F’ ma non in F
dove
f(
![]() )
è il numero di occorrenze pesate di
)
è il numero di occorrenze pesate di
![]() in F, un'occorrenza
in F, un'occorrenza
![]() in una clausola binaria essendo
contata come 5
in clausole di lunghezza 4,... Il fattore esponenziale 5
è fissato empiricamente ed è migliore, nella sperimentazione di Li e Ambulagan,
di 2 -
il fattore
utilizzato nella regola Jeroslow-Wang [68].
in una clausola binaria essendo
contata come 5
in clausole di lunghezza 4,... Il fattore esponenziale 5
è fissato empiricamente ed è migliore, nella sperimentazione di Li e Ambulagan,
di 2 -
il fattore
utilizzato nella regola Jeroslow-Wang [68].
Li
e Ambulagan hanno comparato Satz con CSAT, Tableau, e POSIT, le altre tre
procedure DPL fra le migliori nella letteratura per i problemi 3SAT random difficili. I problemi 3SAT sono generati utilizzando il metodo di Mitchel e
al. [98
] da 4 serie di n
variabili e m
clausole con il rapporto m/n=4.25,
n in passi da 50
tra 250 variabili e 400
variabili. I problemi 3SAT random generati con il rapporto m/n=4.25
sono i più difficili da risolvere.
Li
e Ambulagan hanno utilizzato un eseguibile del CSAT del luglio 1996. La
versione di Tableau utilizzata è chiamata 3tab
ed è la stessa utilizzata per la sperimentazione presentata in [16].
POSIT è stato compilato utilizzando il make fornito, su una workstation Sun SPARC20 dal source chiamato posit-1.0.tar.gz [1]. Le Tabelle 8.2 e 8.3 mostrano che le performance delle 4 procedure DPL sui problemi 3SAT random difficili con 250, 300, 350 e 400 variabili, dove time - run-time medio reale si ottiene dal comando unix /usr/bin/time e t_size - la dimensione dell’albero di ricerca è riportata o calcolata dal numero di rami riportati dalla procedura DPL. Notiamo che nessuna delle procedure CSAT, POSIT, 3tab e Satz utilizza il backjumping.

Tabella 8.2: Run-time medio (in secondi) e la dimensione media dell’albero di ricerca del C-SAT, Tableau, POSIT e Satz per un rapporto m/n=4.25 per problemi soddisfacibili
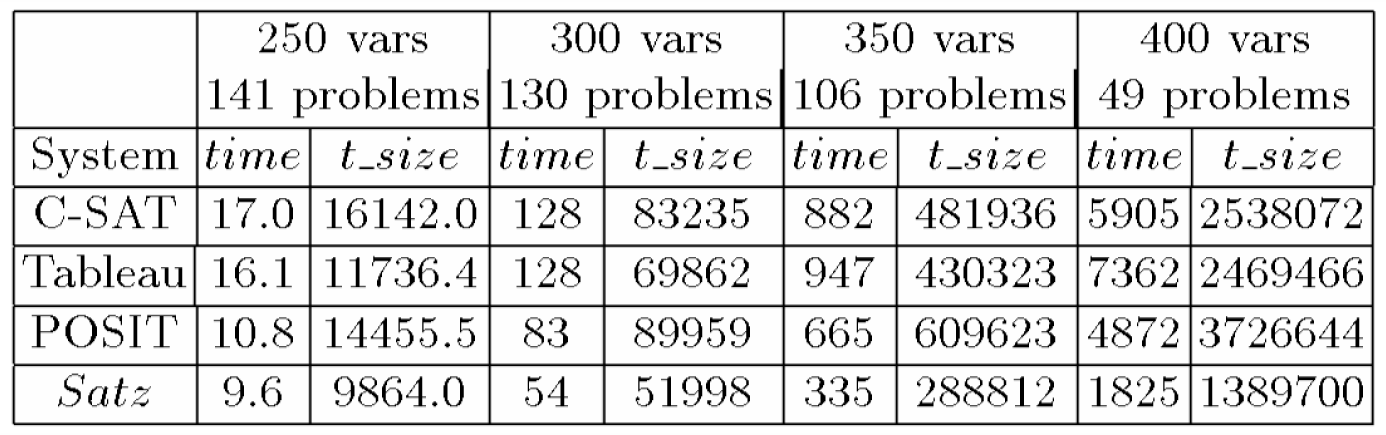
Tabella 8.3: Run-time medio (in secondi) e
la dimensione media dell’albero di ricerca del C-SAT, Tableau, POSIT e Satz
per un rapporto m/n=4.25 per problemi non soddisfacibili
Le Tabelle 8.2 e 8.3
mostrano che sui problemi 3SAT
random difficili, Satz è più veloce delle sopra citate versioni di CSAT,
Tableau e POSIT, la dimensione dell’albero di ricerca per il Satz è la più
piccola, e il run-time e la dimensione dell'albero di ricerca del Satz crescono
più lentamente. Tabella 8.4 nostra che il vantaggio di Satz comparato con le
versioni citate di CSAT, Tableau e POSIT al rapporto m/n=4.25.
Ogni
voce è calcolata dalle Tabelle 8.2 e 8.3 (media di tutti i problemi in un
punto) utilizzando la seguente equazione:
gain=(value(system)/value(Satz)-1)*100%
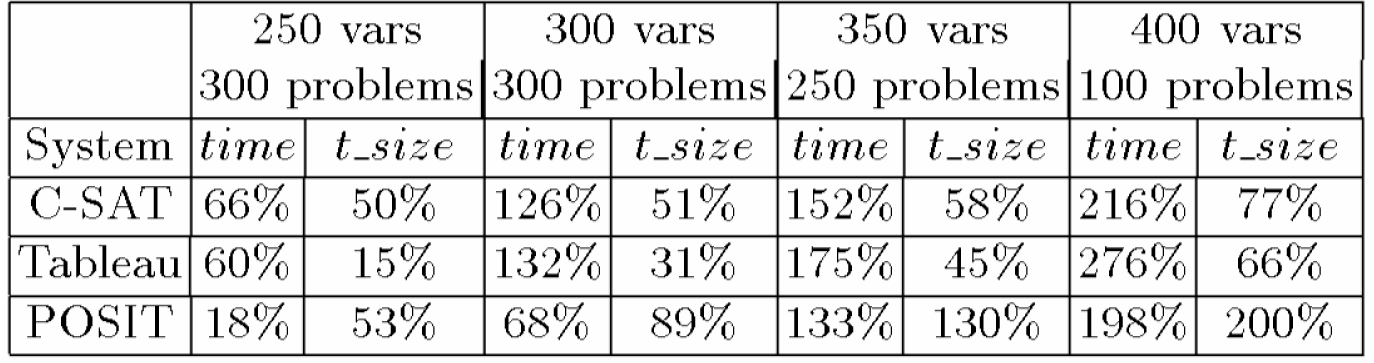
Tabella
8
.4: Il guadagno di Satz rispetto a C-SAT, Tableau, POSIT in termini di
run-time medio (in secondi) e la dimensione media dell’albero di ricerca per
un rapporto m/n=4.25 calcolato dalle Tabelle 8.2 e 8.3
dove value è la media reale del run-time o la media reale della
dimensione del albero di ricerca e system
è CSAT, Tableau o POSIT. Dalla Tabella 8.4, risulta chiaro che il vantaggio
del Satz cresce con la dimensione della formula in ingresso.
Compariamo
Satz con le altre tre procedure DPL (POSIT, GRASP e relsat(4)) fra le migliore
nella letteratura per i problemi SAT strutturati, dove GRASP e POSIT sono le due
migliori in [17] comparate con CSAT,
Tableau, H2R , SATO, TEGUS sui benchmark DIMACS e UCSC e relsat(4) è la
procedura migliore esaminata in [6]. Li e Ambulagan hanno utilizzato 4 ben conosciuti benchmark per i
problemi SAT strutturati:
·
DIMACS
[2];
·
UCSC
[3];
·
i
problemi Beijingchallenging [4];
·
i
problemi di pianificazione proposti da Kautz e Selman [5].
La versione del POSIT è la stessa dell'ultima sezione. Li e Ambulagan hanno utilizzato un eseguibile del sistema GRASP (la versione del maggio 1996) disponibile da Joao M. Silva. Il relsat(4) system V1.00 sono stati ricevuti da Roberto J. Bayardo Jr.
Seguendo
Hooker & Vinay [65] e Silva & Sakallah [117], Li e Ambulagan hanno utilizzato un tempo di cutoff
(2 ore) come un sostituto per il run-time reale e suddiviso
i benchmark DIMACS e UCSC in classi, per esempio la classe aim100
include tutti i problemi con il nome aim100*.
In ogni classe, #M
denota
il numero totale di membri della classe, mentre #S
il numero di problemi risolti efficacemente dalla procedura DPL corrispondente
in meno di due ore. Time
rappresenta il tempo totale CPU in secondi impiegati per trattare tutti i membri
di una classe - un problema che non può essere risolto in meno di 2
ore contribuisce con 7200 secondi al tempo totale. Li e Ambulagan non hanno
incluso le classe F, G, PAR32 e Hanoi5 che nessuno degli algoritmi Satz, GRASP,
POSIT e relsat(4) riesce a risolvere in meno di 2
ore. I problemi difficili di Beijing e i problemi di pianificazione sono
elencati individualmente e un problema che non può essere risolto in meno di 2 ore è marcato da >7200.
I risultati ottenuti sono mostrati nelle Tabelle 8.5, 8.6, 8.7 e
8.8.
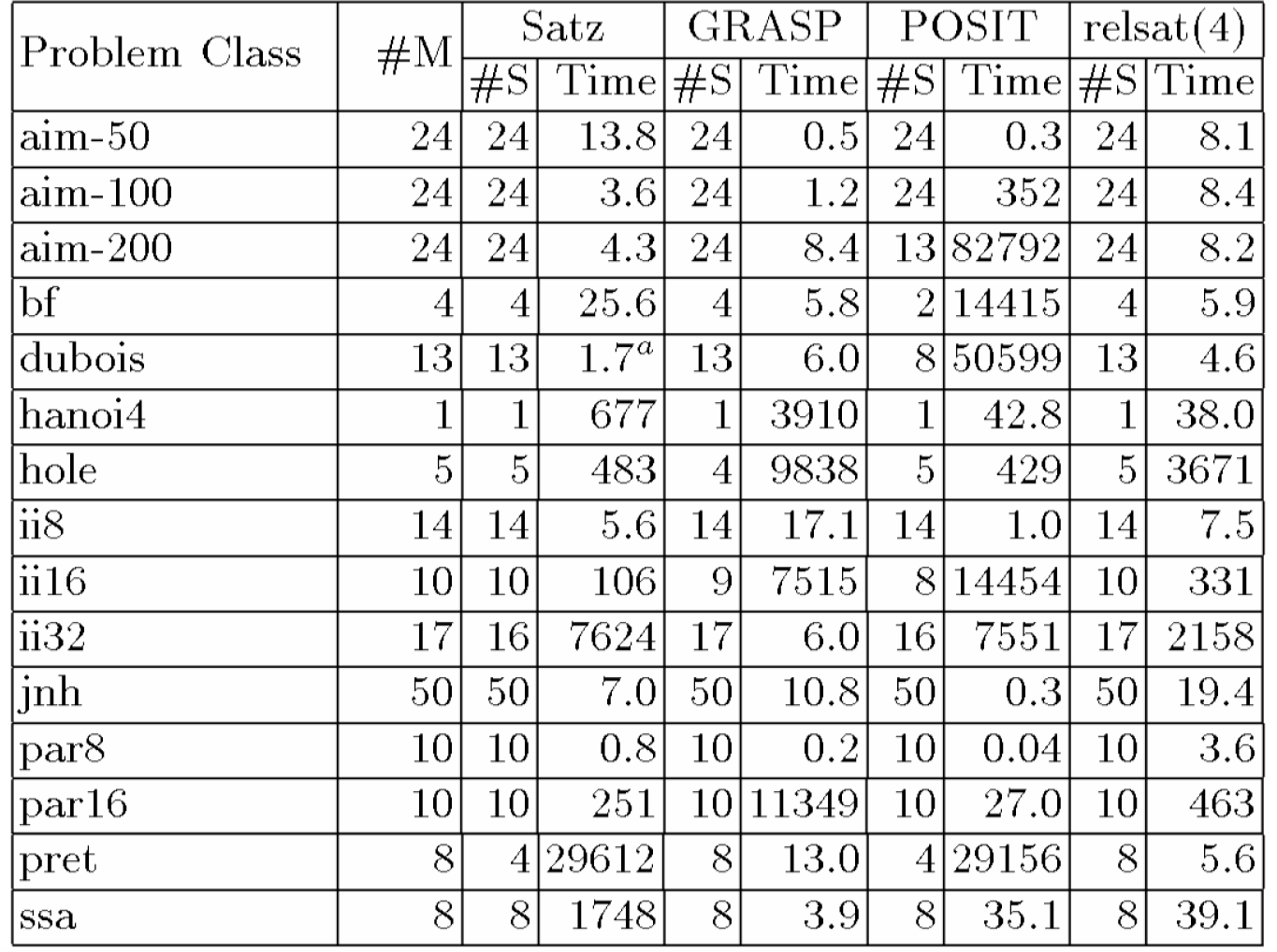
Tabella 8.5: Run-time totale (in secondi) dei problemi DIMACS
Una
prima osservazione è che Satz, GRASP, relsat(4) sono tutte significativamente
migliori del POSIT su questi benchmark. In seguito Li e Anbulagan
hanno analizzato soltanto le performance di Satz, GRASP e relsat(4).
Li
e Ambulagan hanno trovato che Satz è comparabile con relsat(4) e GRASP su più
problemi DIMACS e UCSC (un totale di 22
classi) eccetto la classe pret
dove non c'è nessuna soluzione di lunghezza £ 3 e la maggior parte delle variabili sono simmetriche così
che l’euristica UP fallisce nel distinguerli. Satz è significativamente
migliore del GRASP e relsat(4) in 3
classi (hole,
ii16,
par16)
e per 12 classi aim50,
aim100,
aim200,
bf,
dubois,
ii8,
jnh,
par8,
bf0432,
ssa0432,
ssa6288
e ssa7552,
ha delle performance equivalenti. Satz è anche molto efficace su più problemi ssa
e bf,
eccetto un piccolo numero fra loro (8
ssa
su 102 e 3
bf
su 223) dove per Satz aumenta il tempo totale per risolvere le
corrispondenti classi.
Per esempio, mentre la maggior parte dei problemi della classe bf1355 possono essere risolti entro 3 secondi, il problema bf1355243 impiega 1395 secondi per essere risolto. Il problema più difficile per Satz nelle classi ssa e bf è bf2670-244 su cui impiega 3 ore e 47 minuti per essere risolto.
Nel banchmark
Beijing, Satz risolve lo stesso numero di problemi come relsat(4) e uno in più
del GRASP. Sui problemi di pianificazione di Kautz e Selman, Satz è anche
comparabile con GRASP e relsat(4) eccetto 4
problemi su 31. Notiamo che Satz contiene un pre-processing della
formula CNF d’ingresso per cancellare le clausole duplicate, le tautologie, e
i letterali duplicati nelle clausole, che rappresentano un consumo di tempo per
i problemi grandi come i problemi di pianificazione di Kautz e Selman o alcuni
problemi Beijing difficili che contengono più di 100.000
clausole e non sono trascurabili specialmente quando la stessa ricerca impiega
poco tempo.
In
termini di CSP, Satz adopera essenzialmente qualche semplice tecnica look-ahead
per raggiungere al più presto possibile ad un dead end: un'euristica di
ordinamento delle variabili (euristica UP), un controllo di consistenza in
avanti (Unit propagation) e un pre-processing semplice, l’euristica essendo se
stessa basata sul controllo della consistenza in avanti. Comunque, Satz non
include tecniche look-back come backjumping ed apprendimento, un’altra classe
di tecniche per i problemi CSP.
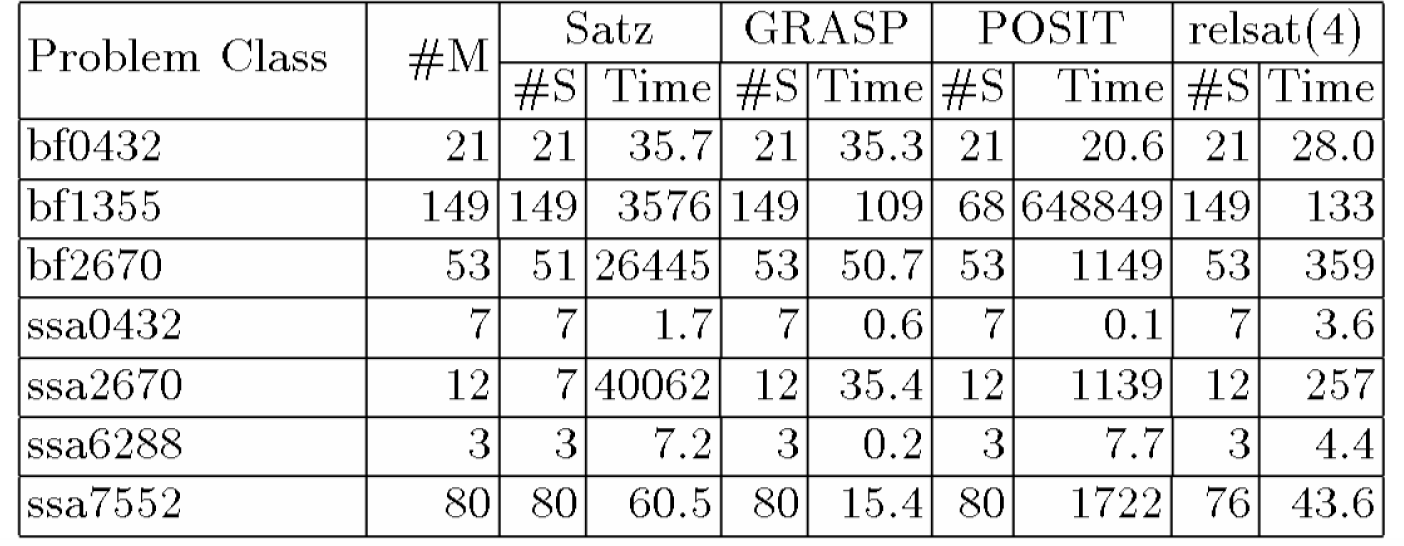
Tabella 8.6: l run-time totale(in secondi) dei problemi UCSC
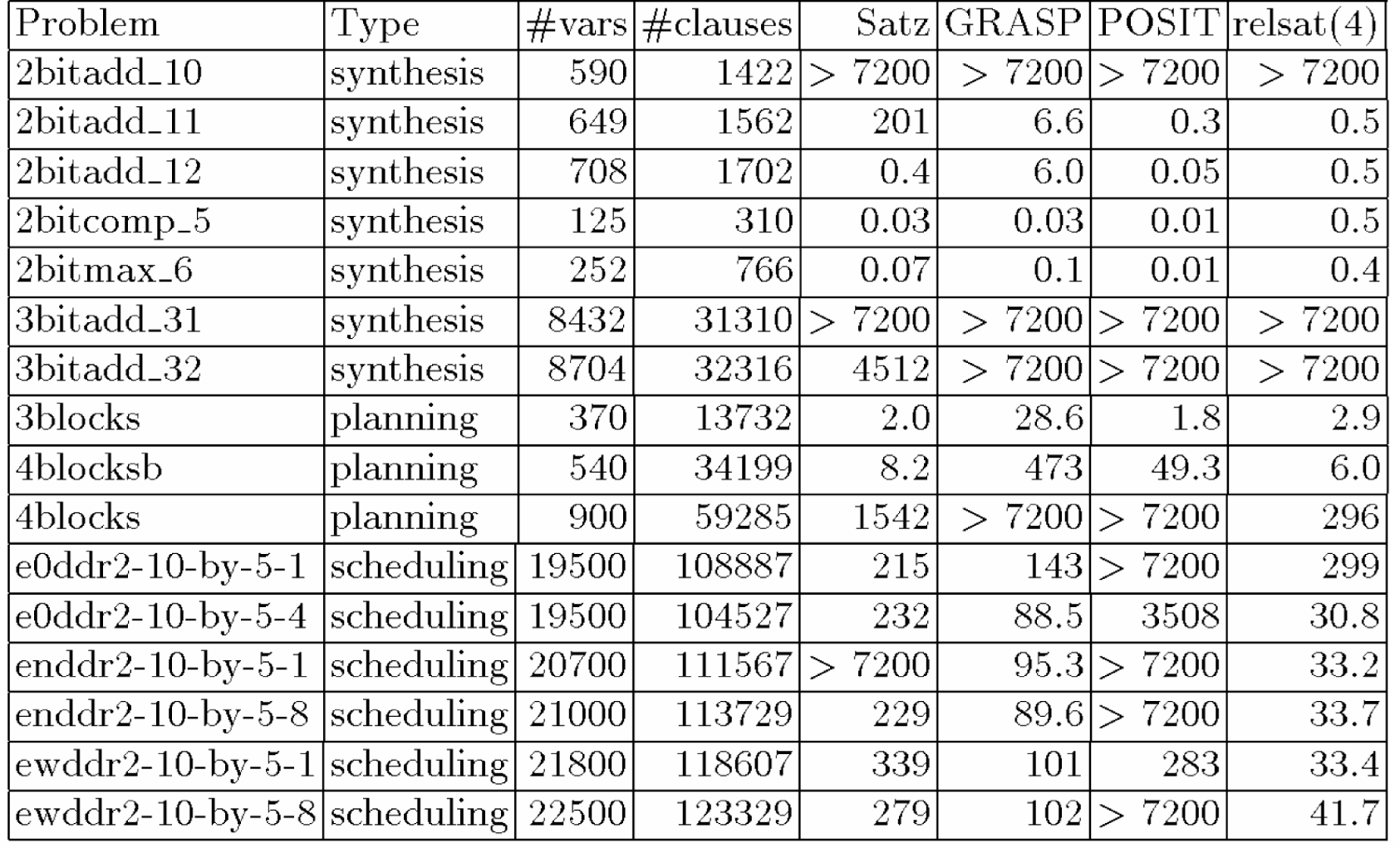
Tabella
8
.7: I run-time (in secondi) dei problemi Beijing
L'euristica del
GRASP si può spiegare dall'ipotesi di soddisfazione, che intende soddisfare
direttamente il numero più grande di clausole, mentre per il relsat(4)
dall’ipotesi di semplificazione, che intende valutare il maggior numero di
variabili quando ramifica. La loro euristica con ordinamento è più semplice di
quella del Satz. Comunque loro sfruttano un backjumping sofisticato ed
apprendimento per affrontare i problemi SAT strutturati. I risultati
sperimentali presentati nell'ultima sezione suggeriscono che le buone
performance del GRASP e relsat(4) su molti problemi SAT strutturati possono
essere raggiunte semplicemente da una risoluzione limitata in cima all'albero di
ricerca ed un’ottima euristica UP. L'ultimo approccio ha i vantaggi di essere
più semplice e molto più efficace per i problemi 3SAT
random.
Un’euristica migliore per l’ordinamento delle variabili permette di evitare molte backtracking inutili. Siano xi1,xi2,…xib,…xid le traiettorie dall'origine al dead end in un albero di ricerca DPL, il backtracking cronologico standard retrocede verso xid-1, mentre il backjumping potrebbe saltare a xib nel caso quale le variabili xib+1,…xid-1 non contribuiscono al conflitto scoperto in xid, evitando in questo modo il tempo per esplorare una regione inutile dello spazio di ricerca. Comunque se guardiamo più attentamente al caso, troviamo che se il backjumping permette di evitare l'esplorazione inutile, è perché le variabili di ramificazione xib+1,…xid-1 non sono buone. Se l'euristica di ordinamento delle variabili sceglie xid come variabile di ramificazione immediatamente dopo xib il backjumping potrebbe essere semplicemente backtracking cronologico.
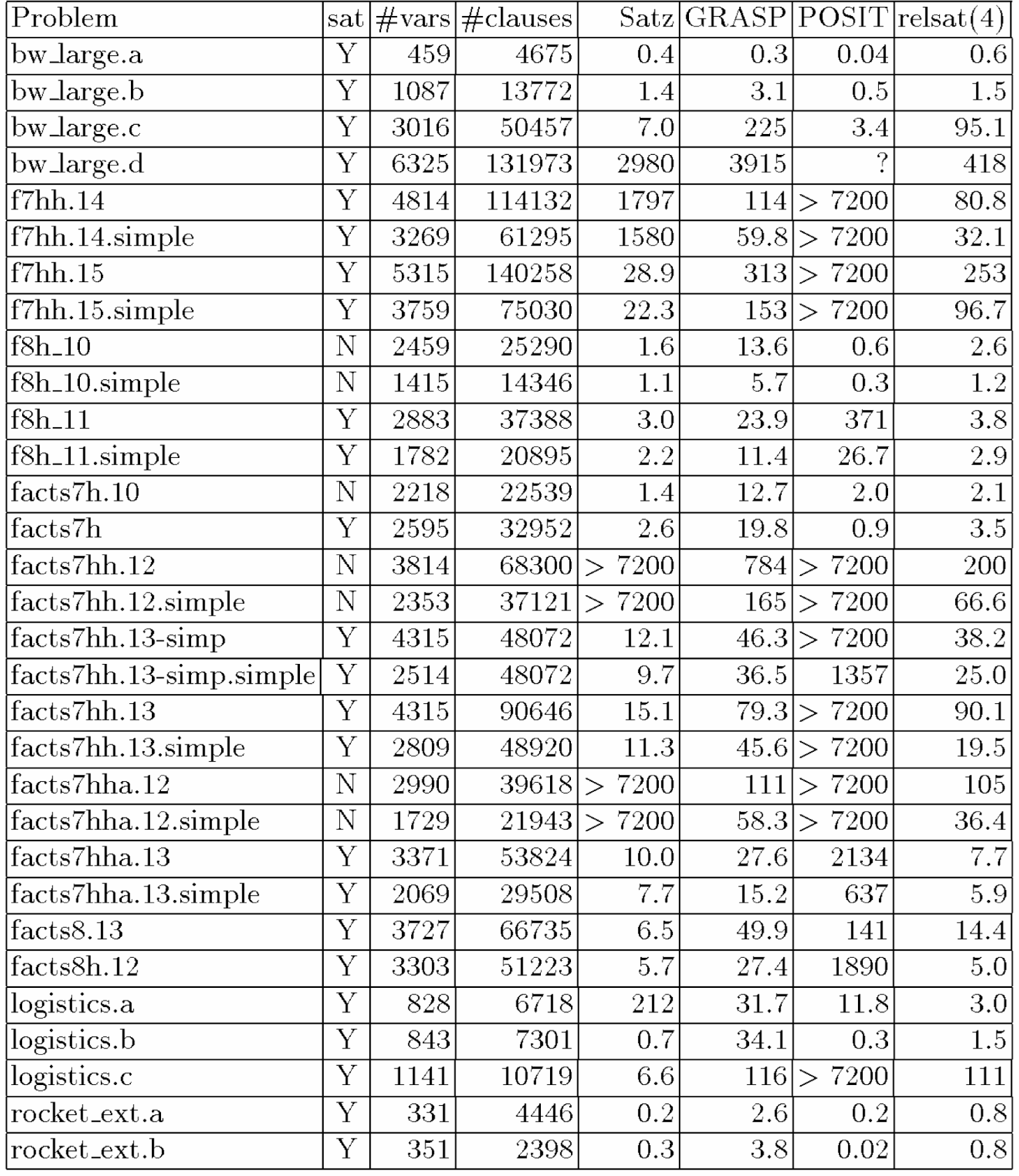
Tabella 8.8: I run-time (in secondi) dei problemi di
pianificazione di Kautz e Selman
Chiaramente
l'euristica UP permette a Satz di fare a meno del backjumping in maggior parte
dei casi.
Satz
non include alcuna delle tecniche di apprendimento classiche applicate durante
la ricerca. Ma Satz include un apprendimento
statico
standard che consiste in una risoluzione limitata prima della ricerca per
aggiungere alcune soluzioni di lunghezza £ 3 nel database della clausola. Una ricerca completa di
tutte le soluzioni di lunghezza £ 3 prima della
ricerca permettono di risolvere istantaneamente tutti i problemi della classe dubois,
mentre l’apprendimento
statico
standard rende Satz due volte più veloce. D'altra parte, molti problemi come ssa*
e ii*
potrebbero esplodere la memoria del computer per una ricerca completa di tutte
le soluzioni di lunghezza £
3.
Sembra
promettente un'integrazione
accurata con un modesto overhead dell’euristica UP ed un apprendimento
dinamico come quello proposto in relsat(4).
Sembra
che le tecniche look-back, come descritte in GRASP e relsat(4), non siano
appropriate per i problemi 3SAT
random. Per esempio, la Tabella 8.9 mostra il comportamento del relsat(4) e del
GRASP sui problemi 3SAT random difficili confrontati con Satz.
D'altra parte, le tecniche look-ahead come quelle implementate in Satz possono essere utilizzate per affrontare i problemi 3SAT random e molti problemi SAT strutturati. Se una tecnica è potente per i problemi SAT random, probabilmente è potente per problemi SAT strutturati.
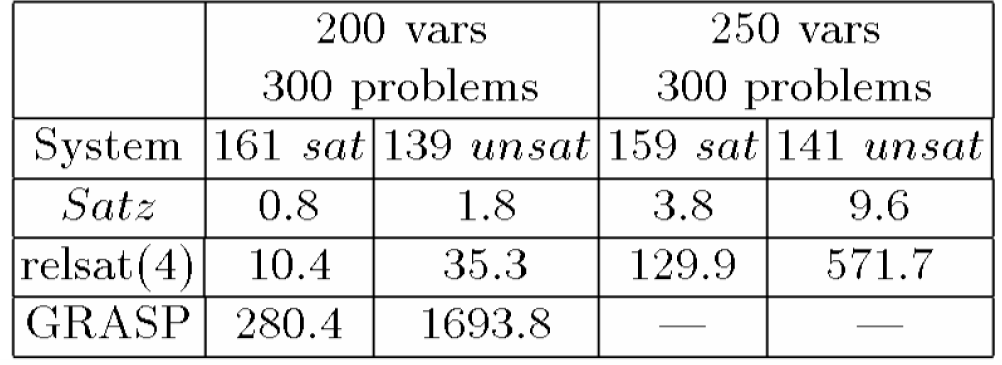
Tabella 8.9: Run-time medio (in secondi) di Satz, relsat(4) e
GRASP per il rapporto m/n=4.25
La strategia essenziale per scrivere una procedura DPL è di provare a raggiungere al più presto possibile ad un dead end e le euristiche sono probabilmente, i metodi più efficaci per realizzare la strategia. Comunque, se l’euristica fallisce nel lavorare bene, per esempio, per i problemi dove la maggior parte delle variabili sono simmetriche, si dovrebbero provare altri metodi, come l’apprendimento o simmetry detection. In questo senso, Satz può essere ancora migliorata nel futuro.
[2] disponibile a ftp://dimacs.rutgers.edu/pub/challenge/satisfiability
[3] disponibile a ftp://dimacs.rutgers.edu/pub/challenge/sat/contributed/UCSC
[4] disponibile a http://www.cirl.uoregon.edu/crawford/beijing
[5] disponibile a ftp://ftp.ricerca.att.com/dist/ai/logistics.tar.Z
| Indietro | ||
| Relsat |
SAT solver |
Novelty |