
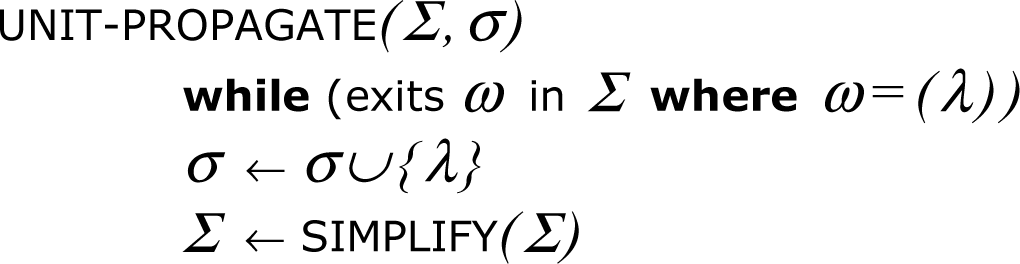
| Indietro | ||
Bayardo e Schrag hanno presentato una versione migliorata della procedura DavisPutnam per la soddisfacibilità proposizionale SAT su esempi ricavati dai problemi del mondo reale nella pianificazione, scheduling, diagnosi e sintesi dei circuiti. Gli autori hanno mostrato che incorporando tecniche CSP look-back, specialmente la nuova tecnica dell'apprendimento relevance-bounded, trasformano molti problemi facili che altrimenti sarebbero oltre la portata del DP. Frequentemente loro fanno che l’algoritmo sistematico DP, lavori altrettanto bene o meglio degli algoritmi SAT stocastici come GSAT o WSAT.
Come
gia mostrato, la soddisfacibilità proposizionale CNF SAT è uno specifico
problema con soddisfacimento di vincoli CSP. Fino poco tempo fa ci sono state
poche applicazioni delle tecniche CSP look-back negli algoritmi SAT. Nel lavoro
precedente, Bayardo e Schrag [4] hanno dimostrato che la versione look-back-enhanced
dell’algoritmo Tableau per le istanze 3SAT [16] può risolvere facilmente molte istanze che senza il look-back
sarebbero eccezionalmente
hard,
più difficili di altri esempi con le stesse caratteristiche di superficie.
Nella
presentazione del Relsat, le istanze sono state generate artificialmente. Bayardo
e Schrag hanno
dimostrato l'utilità pratica delle tecniche CSP lookback utilizzando un nuovo
algoritmo look-back-enhanced riferito a Tableau per risolvere istanze SAT grandi
derivate da problemi di pianificazione del mondo reale, scheduling e diagnosi e
sintesi dei circuiti. Kautz e Selman [78] avevano trovato Tableau inadeguato per risolvere molte istanze
derivate dalla pianificazione e sono ricorsi ad utilizzare un algoritmo
stocastico, WSAT anche noto come WalkSAT [114].
Data la solita struttura della ricerca backtrack per le soluzioni sistematiche del problema con soddisfacimento di vincoli CSP, le tecniche progettate per migliorare l’efficienza possono essere divise in due classi:
·
tecniche di look-ahead che sfruttano informazioni riguardo lo
spazio di ricerca rimanente;
·
tecniche lookback che sfruttano le informazioni sulla ricerca che
ha avuto già luogo.
La prima classe include l’euristica con ordinamento delle variabili e schemi dynamic consistency enforcement come il forward checking.
La seconda classe include schemi per il backjumping (noto anche come intelligent backtracking) ed apprendimento (noto anche come nogood o constraint recording).
Negli algoritmi CSP, sono popolare tecniche dalle entrambe classi; per esempio, una combinazione comune di tecniche è forward checking, conflict-directed backjumping, e un ordening heuristic preferring variables con i domini minori.
SAT
è un genere specifico di CSP, in cui ogni variabile prende i valori {True,
False}. Gli algoritmi sistematici più popolari per il SAT sono versioni
della procedura DavisPutnam [19]. In termini di CSP, DP è equivalente alla ricerca backtrack con
forward checking e un ordering heuristic favoring unit-domained variables. Due
moderne realizzazioni efficaci sono Tableau [16] e POSIT [26]; le entrambe sono estremamente ottimizzate ed includono euristiche
con ordinamento di variabili selezionate attentamente.
Gli
algoritmi di ricerca sistematica o globale attraversano lo spazio di ricerca
sistematicamente per assicurarsi che nessuna parte rimanga inesplorata. Loro
sono completi: avendo a disposizione
abbastanza run-time, se esiste una soluzione loro la troveranno; se non esiste
nessuna soluzione loro riporterà questo.
L’alternativa
agli algoritmi sistematici per SAT sono gli algoritmi stocastici o algoritmi di
ricerca locale come WSAT e GSAT [116], come abbiamo visto precedentemente. Gli algoritmi stocastici
esplorano lo spazio di ricerca in modo casuale, facendo perturbazioni locali ad
un assegnamento di lavoro senza memoria dove loro sono stati. Loro sono incompleti: non garantiscono di trovare una soluzione se esiste una; se non
trovano nessuna soluzione, non possono concludere che non esiste nessuna.
Gli
algoritmi stocastici migliorano rispetto a quelli sistematici su istanze
soddisfacibili dalla regione phase transition dello spazio dei problemi casuali,
come il 3SAT
random. Le istanze in questa regione sono mediamente più difficili per diversi
algoritmi; loro cominciano ad essere utilizzati frequentemente come benchmark
per le performance degli algoritmi SAT. Nello stesso tempo è riconosciuto che
loro hanno strutture fondamentali molto diverse dalle istanze SAT.
Gli
algoritmi stocastici migliorano anche rispetto agli algoritmi sistematici come
Tableau su alcuni problemi del mondo reale. Molti problemi di pianificazione
codificati in SAT descritti da Kautz e Selman [78] sono irrealizzabili per Tableau (10 ore), ma sono risolti facilmente dal WSAT (circa 10 minuti). La versione DP look-back-enhanced di Bayardo e
Schrag è competitiva con WSAT nell'identificare piani fattibili utilizzando le
stesse istanze. Inoltre, DP look-back-enhanced dimostra l'inesistenza dei piani
corti da 1
a 3 minuti su istanze che Tableau non riesce a risolvere in 10 ore; questo compito è impossibile per WSAT, dovuto alla
sua incompletezza.
Per
un CNF dato, Bayardo e Schrag hanno rappresentato un assegnamento come un set di
letterali ognuno dei quali è soddisfatto. Un nogood
è un assegnamento parziale che non soddisferà il CNF dato. La clausola (aÙ
bÙØc)codifica
il nogood {Øa,Øb,c
}. Chiameremo
tale clausola codificata nogood un reason.
La risoluzione è l'operazione che consiste nel combinare due clausole in
ingresso menzionando un letterale dato e la sua negazione, ricavando una
clausola implicita che menziona oltre questi tutti gli altri letterali.
La procedura DavisPutnam DP è rappresentata sotto in pseudo-codice. SAT è un problema di decisione, sebbene frequentemente noi siamo interessati ad esibire anche un assegnamento di verità soddisfacente s, che è vuoto partendo con l'entrata iniziale al livello superiore fino al ricorrente, procedura DP call-by-value.
 |
|
La
formula CNF S
e l'assegnamento di verità s
sono modificati in chiamate per nome nell’UNITPROPAGATE. Se S
contiene una contraddizione, questo è fallimento ed è necessario il
backtracking. Se tutte le sue clausole sono già state semplificate, allora
l'assegnamento corrente soddisfa la formula CNF.
SELECTBRANCHVARIABLE
è una funzione euristica che ritorna la prossima variabile al valore
nell’elaborazione dell'albero di ricerca. Se nessun valore di verità
funziona, anche questo è fallimento.
UNITPROPAGATE
aggiunge il singolo letterale l
da una clausola unità
![]() al set di letterali s,
poi semplifica la formula CNF rimovendo qualsiasi clausola nella quale si
presenta l, e accorciando tutte le clausole in cui Øl
si presenta attraverso la risoluzione.
al set di letterali s,
poi semplifica la formula CNF rimovendo qualsiasi clausola nella quale si
presenta l, e accorciando tutte le clausole in cui Øl
si presenta attraverso la risoluzione.
Le
versioni moderne del DP, incluso POSIT e Tableau, incorporano unit propagators
altamente ottimizzati, ed euristiche sofisticate per selezionare le variabili di
ramificazione. L’euristica per selezionare le variabili di ramificazione
utilizzata dall’implementazione di Bayardo e Schrag è
inspirata dall’euristica del POSIT e del Tableau, sebbene è piuttosto
semplice ridurre il carico dell’implementazione.
Dettagli
della selezione della variabile di ramificazione sono come segue.
Se
non ci sono clausole binarie, selezionare una variabile di ramificazione in modo
random. Altrimenti, assegnare ad ogni variabile g apparsa in alcune clausole binarie un punteggio neg(g)×pos(g)+neg(g)+pos(g)
dove neg(g) e pos(g) sono i numeri delle occorrenze di g e Øg in tutte le clausole binarie.
Raggruppare
tutte le variabili all'interno del 20%
del miglior punteggio in un set candidato.
Se
ci sono più di 10 candidati, rimuovere le variabili a caso
finché rimangono solamente 10.
Se c'è solamente un candidato, è ritornato come variabile di ramificazione.
Altrimenti,
ogni candidato è punteggiato di nuovo come segue. Per un candidato g, calcolare pos(g) e neg(g) come il numero di variabili valutato da UNITPROPAGATE dopo aver
fatto l'assegnamento {g} e rispettivamente
{Øg}. Probabile che le entrambe unit propagation portino ad una
contraddizione, ritornare immediatamente g
come la prossima variabile di ramificazione e seguire l’assegnamento per
questa variabile che porta alla contraddizione. Altrimenti, accordare un
punteggio a g utilizzando la stessa funzione come sopra. Ogni candidato deve
essere punteggiato senza trovare una contraddizione, selezionare a caso una
variabile di ramificazione da quelle candidato all'interno del 10%
dei migliori punteggi.
Eccetto
i casi di contraddizione notati sopra, il primo valore di verità assegnato ad
una variabile di ramificazione è selezionato a caso. Bayardo e Schrag hanno
applicato le randomizzazioni descritte solamente dove l’euristica tradizionale
non è riuscita migliorare sostanzialmente attraverso le varie istanze.
Il
pseudo-codice del DP di sopra realizza un backtracking semplice mediato da una
stack con una funzione ricorrente. Il conflict directed backjumping CBJ [107
] ritorna attraverso questo stack astratto in una maniera non
sequenziale, dove possibile, saltellando per motivi d’efficienza i frame di
stack. Il suo meccanismo richiede l'esaminazione degli assegnamenti fatti da
UNIT-PROPAGATE, non solo assegnamenti a variabili di ramificazione, quindi è più
complicato di quello che potrebbe rappresentare lo pseudo-codice DP.
Bayardo
e Schrag hanno implementato il CBJ avendo UNITPROPAGATE che mantiene un
pointer alla clausola nell’ingresso CNF che serve come reason per escludere di
considerare un particolare assegnamento.
Per
esempio, quando {Øa,Øb}
è parte del assegnamento corrente, la clausola di ingresso (aÚ
bÚ
x)
è il reason per escludere l'assegnamento {Øx}. Ogni qualvolta si ha una contraddizione, sappiamo che qualche
variabile ha entrambi i valori di verità non ammessi. Per questo fallimento il
CBJ costruisce un working reason C
risolvendo
le due rispettive reason; poi indietreggia alla variabile d
più recentemente assegnata in C. Supponiamo che {g} è stato l'assegnamento più recente della variabile g.
Se {Øg} è esclusa dalla reason D,
allora creiamo un nuovo working reason E
risolvendo C e D
e si indietreggia alla variabile più recentemente assegnata in E.
Altrimenti, installiamo C come la reason per escludere {g}, cambiare l'assegnamento corrente per includere {Øg}, e procediamo con la DP.
Estendendo
il nostro esempio, supponiamo che nel trovare l’errore abbiamo la reason
complementare (aÚ
bÚ
Øx),
e che b è stato assegnato dopo a. La risoluzione ci dà il working reason (aÚ
b),
così CBJ indietreggia dove è stato fatto l'assegnamento {Øb}. Se {b}
è escluso, supponiamo che il reason è {ØbÚ
y}. La risoluzione fornisce il nuovo working
reason (aÚ
y)
e CBJ lo mantiene. Se {b}
non è escluso (b era un variabile di ramificazione), (aÚ
b)
diventa la reason escludendo {Øb}, e {b}
sostituisce {Øb} nell’assegnamento corrente prima che la DP continui.
Gli
schemi con apprendimento mantengono derived reason più lunghe di quanto fa il
CBJ, che può scartarli appena loro non indicano più un valore come escluso.
L'apprendimento senza restrizioni memorizza ogni derived reason esattamente come
se fosse una clausola dall'istanza fondamentale, permettendo che sia utilizzato
per il resto della ricerca. In quanto l’overhead dell'apprendimento senza
restrizioni è alto, Bayardo e Schrag hanno applicato solamente gli schemi con
apprendimento limitato come definito in [5]. L'apprendimento size-bounded dell’ordine i mantiene indefinitamente solamente quelli derived reason che
contengono
![]() o meno variabili. Ad esempio, la
reason (aÚ
b)
sarebbe mantenuta dall'apprendimento size-bounded del secondo ordine, ma reason
più lunghi non potrebbero. L'apprendimento relevance-bounded dell'ordine
o meno variabili. Ad esempio, la
reason (aÚ
b)
sarebbe mantenuta dall'apprendimento size-bounded del secondo ordine, ma reason
più lunghi non potrebbero. L'apprendimento relevance-bounded dell'ordine
![]() mantiene ogni reason che contiene
al massimo
mantiene ogni reason che contiene
al massimo
![]() variabili i cui l'assegnamenti sono
stati cambiati da quando la reason è stata ricavata. Per esempio, supponiamo
che stiamo effettuando l’apprendimento relevance-bounded del secondo ordine, e
deduciamo una reason (aÚ
bÚ
y)
dove le variabili a,
b e y
sono state assegnate nell'ordine in cui appaiono. Questo reason sarebbe
mantenuto dall’apprendimento relevance-bounded del secondo ordine finché a rimane assegnata come Øa. Appena a
è re-assegnata o dis-assegnata da un ripristino, la reason sarebbe scartata.
variabili i cui l'assegnamenti sono
stati cambiati da quando la reason è stata ricavata. Per esempio, supponiamo
che stiamo effettuando l’apprendimento relevance-bounded del secondo ordine, e
deduciamo una reason (aÚ
bÚ
y)
dove le variabili a,
b e y
sono state assegnate nell'ordine in cui appaiono. Questo reason sarebbe
mantenuto dall’apprendimento relevance-bounded del secondo ordine finché a rimane assegnata come Øa. Appena a
è re-assegnata o dis-assegnata da un ripristino, la reason sarebbe scartata.
Bayardo
e Schrag hanno utilizzato tre serie di test separati per comparare le
performance del DP look-back-enhanced con altri algoritmi le cui performance
sono state riferite per gli stessi esempi: istanze di pianificazione codificate
SAT da Kautz e Selman [1];
istanze di pianificazione e diagnosi di circuiti selezionate dal DIMACS
Challenge associate con la competizione SAT del 1993 [2]
ed istanze di pianificazione, scheduling e sintesi di circuiti dalla
competizione SAT di Beijing del 1996 [3].
Le
istanze di pianificazione codificate SAT costruite da Kautz e Selman [78] sono
elencate nella Tabella 7.1.
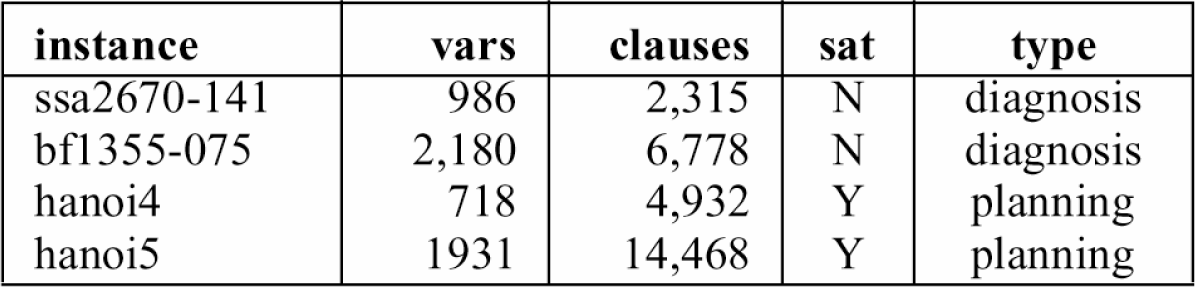
Tabella 7 .1: Le istanze di pianificazione di Kautz e Selman
Le
istanze log corrispondono ai problemi di pianificazione nella logistica; le
istanze bw sono per il blocsworld che sono tuttavia difficili. Le istanze
gp
sono codifiche Graphplan, le istanze dir
codifiche dirette (statebased per le istanze di logistica, lineare per blocks
world), e le istanze un sono codifiche Graphplan non soddisfabili per dimostrare la non
fattibilità dei piani corti.
Nella
serie DIMACS, Bayardo e Schrag hanno scelto le istanze per la diagnosi dei
circuiti di Van Gelder e Tsuji ssa (single-stuck-at) e bf
(bridge-fault), e le istanze di pianificazione torre di Hanoi di Selman che
utilizzano anche esse codifica lineare. Brevemente, riportiamo solamente le più
difficili, per tutti gli algoritmi investigati delle istanze single-stuck-at e
bridge-fault (mostrato nella Tabella 7.2).

Tabella 7 . 2: Le istanze DIMACS
Tabella
7
.3: Le istanze Beijing
Bayardo e Schrag hanno analizzato tutte le
istanze dalla serie Beijing (vedi Tabella 7.3). Pure le istanze di
pianificazione blocks
utilizzano la codifica lineare. Le istanze di scheduling e
codificano i benchmark di Sadeh come descritto in [17]. Le istanze di sintesi di circuiti bit
sono il contribuito di Bart Selman.
Gli
algoritmi di Bayardo e Schrag sono programmati in C++ utilizzando meno di 2000
linee incluso header files, linee bianche, e commenti [4].
L'implementazione è flessibile, con diverse tecniche look-back e livelli e vari
parametri di compile-time e run-time.
Bayardo
e Schrag non hanno realizzato un’implementazione ottimizzata. Le performance
potrebbero essere migliorate anche utilizzando un’euristica di selezione della
variabile di ramificazione più sofisticata come quella di Freeman e delle
tecniche di pre-processing delle istanze.
Bayardo
e Schrag hanno sperimentato con versioni diverse dell’algoritmo DP. La
versione senza look-back-enhancement è chiamata naivesat,
quella con CBJ soltanto cbjsat, quella a cui è applicato l'apprendimento relevance-size-bounded
del ordine i relsat(i), mentre quella a cui è applicato sizebounded
di ordine i sizesat(i). Bayardo e Schrag hanno utilizzato solamente apprendimento di
ordine 3 e 4, quanto tempo per l’apprendimento di ordine più alto risultava
un overhead, mentre l’apprendimento di ordine più basso aveva poco effetto.
Si
deve avere cura quando si sperimenta con le istanze del mondo reale perché il
numero delle istanze disponibili per la sperimentazione è spesso limitato.
L'esperimento in qualche modo deve permettere che i risultati delle performance
in uno spazio delle istanze limitato di generalizzare ad altre istanze simili.
Bayardo e Schrag hanno trovato la variazione del run-time degli algoritmi che
risolvono la stessa istanza ad essere estremamente alta, dato che sembrano
essere differenze insignificanti nella politica utilizzata nell'ordinare i
valori e le variabili, sia che l'istanza è o no soddisfacibile.
Kautz
e Selman [78
] hanno calcolato la media del run-time su più cicli. Bayardo e
Schrag hanno scelto lo stesso approccio per far girare più volte gli algoritmi
(100)
su ogni istanza con un numero casuale diverso designato ad ogni esecuzione per
assicurare modelli d’esecuzione diversi. Allo scopo di trattare con esecuzioni
che potrebbero prendere un tempo estremamente maggiore, è stato imposto un
tempo limite di 10 minuti se non specificato diversamente, dopo il quale
l'algoritmo usciva con un fallimento. Bayardo e Schrag hanno riportato la
percentuale delle istanze con cui un algoritmo falliva nel risolvere entro il
tempo limite. È stato riportato anche il tempo CPU medio richiesto per
un’esecuzione e qualche volta gli assegnamenti medi delle variabili per
un’esecuzione, facendo la media sulle esecuzioni riuscite.
Gli
esperimenti sono stati realizzati su una workstations SPARC10. Kautz e Selman
[78] hanno riportato i tempi di esecuzione su una SGI Challenge 110MHz.
Per normalizzare
i tempi di esecuzione con quelli di Kautz e Selman per le stesse istanze,
Bayardo e Schrag hanno risolto una serie selezionata di istanze e hanno
comparato la media dei flips
al secondo riportata da WSAT, concludendo che la macchina di Kautz e Selman
è stata 1.6 volte più veloce della loro SPARC10 [5].
Nei risultati sperimentali che seguono, Bayardo e Schrag hanno riportato tutti i
tempi di esecuzione in secondi CPU normalizzati
SPARC10.
Invece di normalizzare i tempi di esecuzione riportati da Kautz e Selman per
Tableau ntab,
Bayardo e Schrag hanno ripetuto gli esperimenti sulla loro macchina, utilizzando
la nuova versione disponibile del Tableau, ntab_back [6]. Questa versione di Tableau incorpora uno schema
di backjumping, e quindi è più simile alla loro cbjsat.
In quanto
ntab_back non incorpora randomizzazioni, i tempi di
esecuzione riportati per quest’algoritmo sono per una singola esecuzione per
ogni istanza.
La Tabella 7.4 nostra le performance per relsat(4), WSAT, e ntab_back sulle
istanze di pianificazione di Kautz e Selman.

Tabella 7.4: Le performance di relsat(4) sulle istanze di pianificazione di Kautz e Selman

Tabella 7.5: Le performance sull’istanza DIMACS bridge-fault bfl355-075
Il
tempo limite è stato 10 minuti per ogni istanza eccetto bw_dir.d,
quindi è stato di 30
minuti. I tempi per WSAT sono quelli riportati da Kautz e Selman [78], normalizzati a secondi CPU SPARC-10. Relsat(4) funziona meglio del
WSAT sulla maggior parte delle istanze. Un'eccezione dove WSAT è chiaramente
superiore è l'istanza log_dir.c che ha determinato il relsat(4) di raggiungere
il tempo limite 22
volte. L'istanza bw_dir.d ha determinato e il relsat(4) di raggiungere il tempo
limite 18 volte, ma gira ancora meglio del WSAT con
vari minuti anche se Bayardo e Schrag hanno considerato 30 minuti per ogni tempo limite del relsat.
Sebbene è difficile arrivare a conclusioni solide sulle performance del
ntab_back quanto tempo il run-time riportato era solamente per una singola
esecuzione, Bayardo e Schrag hanno deciso che relsat(4) è più efficace del
ntab_back sulle istanze per le quali relsat(4) non ha mai raggiunto il limite, e
ancora ntab_back richiede più di 10
minuti per risolvere. Questa include tutte le istanze log_gp e log_un.
Tabella
7.5 mostra le performance delle versioni DP di Bayardo e Schrag sull'istanza
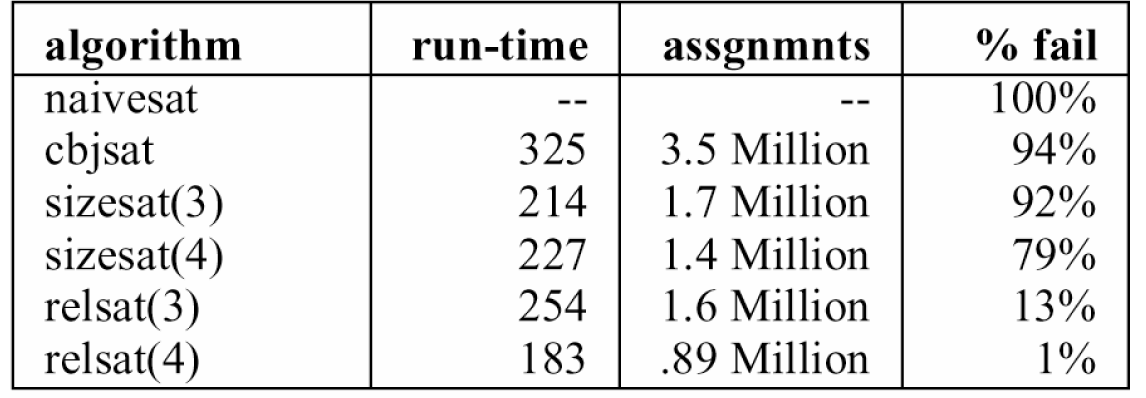
bfl355075 del DIMACS, la più difficile delle istanze bridge-fault. Freeman [26] comunica che POSIT richiede 9.8 ore su una SPARC-10 per risolvere
quest'istanza, mentre Bayardo e Schrag hanno trovato che ntab_back la risolve in
17.05 secondi. La Tabella 7.6 mostra le stesse
informazioni per l'istanza ssa270141 del DIMACS, la più difficile delle
istanze singlestuckat.

Tabella 7.6: Le performance sull’istanza DIMACS single-stuck-at ssa270-141
Freeman
comunica che POSIT necessita 50
secondi per risolvere quest’istanza [7], e Bayardo e Schrag hanno
trovato che ntab_back la risolve in 1.353 secondi. Le entrambe istanze sono non
soddisfacibili.
Naivesat
non è stato capace di risolvere nessuna delle istanze entro 10 minuti in nessuna delle 100 esecuzioni. Aggiungendo CBJ ha risultato che
l'istanza bridge-fault è stata risolta in tutte le 100 runs, ma l'istanza singlestuckat ha
provocato ancora 23
fallimenti. Tutti gli algoritmi di apprendimento hanno eseguito estremamente
bene l'istanza bridge-fault. Per l'istanza singlestuckat, l'apprendimento
relevance-bounded e risultato ancora più veloce.
L'apprendimento
sizebounded del quarto ordine, limitando la dimensione dello spazio di
ricerca, funziona meno bene, dovuto al suo overhead alto, dell'apprendimento
size-bounded del terzo ordine.
Le istanze DIMACS hanoi4 e hanoi5 sembrano contenere minimi locali molto profondi; anche se loro sono soddisfacibili, da quanto si sa, loro non sono stati risolti dagli algoritmi stocastici. Ntab_back risolve hanoi4 in 2,877 secondi ma è stato incapace risolvere hanoi5 entro 12 ore. I risultati delle versioni DP di Bayardo e Schrag su hanoi4 appaiono nella Tabella 7.7.

Tabella 7.7: Le performance sull’istanza
di pianificazione hanoi4
Sebbene
sizesat(4) appare più veloce del relsat(3), il tempo medio di esecuzione è
deviato dovuto al fatto che ha risolto con successo le istanze in soltanto 21% delle esecuzioni. Relsat(3) ha avuto
successo in quasi tutte le esecuzioni e relsat(4) in tutte eccetto una. Hanoi5
è stato risolto soltanto da relsat(4), e solamente in 4 su 100
tentativi. Il tempo medio di esecuzione in queste quattro esecuzioni riuscite è
stato al di sotto dei tre minuti.
Le
versioni DP di Bayardo e Schrag hanno lavorato relativamente bene nella maggior
parte delle istanze Beijing. La tendenza generale è, con più lookback
applicato, si ottengono migliori performance e un'abbassamento della probabilità
di raggiungere il limite. Bayardo e Schrag hanno risolto tutte le istanze
compresi in questa serie senza difficoltà utilizzando relsat(4) con l'eccezione
delle istanze del circuito 3bit
che non è stato mai risolto da alcuna delle loro versioni DP, invece queste
istanze sono state banali per WSAT.
Le
istanze di circuito 2bit
sono state banale (una frazione di secondo per trovare la soluzione) anche per
cbjsat, con l'eccezione di 2bitadd_10, l'unica istanza non soddisfacibile.
Quest’istanza non è stata risolvibile da nessuno degli algoritmi di Bayardo e
Schrag entro 10 minuti. Dopo aver disabilitato il limite,
relsat(4) ha stabilito che era non soddisfacibile dopo 18 ore.
Relsat(4)
ha risolto 4
su 6 istanze di scheduling con 100% percentuale di successo. Due delle istanze,
e010by51 e en10by51 hanno provocato percentuali di fallimento di
21% e rispettivamente 18%. Ripetendo gli esperimenti per queste due
istanze con il limite di 30
minuti sono state ridotte le percentuali di fallimento a 3%
e rispettivamente 1%. Crawford e Baker [17
] hanno reso noto che ISAMP, un algoritmo randomizzato semplice, ha
risolto questi tipi di istanze più efficacemente del WSAT o Tableau.
L’implementazione ISAMP di Bayardo e Schrag ha risolto queste sei
istanze con un ordine di grandezza più rapidamente del relsat(4), e con una
percentuale di successo di 100%, ma non è stato possibile di risolvere
alcun altra istanza dalla serie di test presa in considerazione.
Dalle istanze di pianificazione di Beijing, relsat(3) e relsat(4) hanno trovato facile 3blocks, risolta con una percentuale di successo di 100% mediamente in 6.0 e rispettivamente 6.4 secondi. Anche l'istanza 4blocksb è stata facile, sia relsat(3) che relsat(4) l'hanno risolta con 100% successo, ma questa volta in 79 e rispettivamente 55 secondi. L'istanza 4blocks è stata più difficile. La percentuale di fallimento è stato di 34% per relsat(3) e 17% per relsat(4), con media di secondi CPU di 406 e rispettivamente 333 secondi.
[2] Disponibile a ftp://dimacs.rutgers.edu/pub/challenge/satisfiability
[3] Disponibile a http://www.cirl.edu/crawford/beijing
[4] Source code disponibili a http://www.cs.utexas.edu/users/bayardo
[5] Bayardo e Schrag non son riusciti a ripetere facilmente gli esperimenti di Kautz e Selman sulla loro macchina, a causa della necessità di sintonizzare a mano i tanti parametri del WSAT.
[6] Disponibile a http://www.cirl.uoregon.edu/crawford/ntab.tar
[7] Freeman ha relazionato anche che POSIT esibisce alta variabilità di runtime su ssa2670141, anche se la variazione non è quantificata
| Indietro | ||
| Walksat |
SAT solver |
Satz |