| Indietro | ||
Gli algoritmi di ricerca locale sono stati applicati con successo in molti problemi di ottimizzazione. Generalmente, gli algoritmi di ricerca locale trovano soluzioni buone ma non ottimali, e si credeva che tali algoritmi non potessero essere appropriati per la soddisfacibilità, dove l'obiettivo è di trovare un assegnamento che soddisfa tutte le clausole (se esiste tale assegnamento).
La ricerca locale ha dimostrato di essere efficace nel trovare assegnamenti completamente soddisfacenti per i problemi CNF [3.4], [3.3]. Questi metodi offrono prestazioni migliori rispetto ai più conosciuti algoritmi di ricerca sistematica su certe classi di problemi grandi di soddisfacibilità. Per esempio, GSAT, un algoritmo di ricerca locale a riavvio casuale, può risolvere 3CNF computazionalmente difficili generate random con 2000 variabili, mentre i più veloci algoritmi di ricerca sistematica non possono gestire istanze dalla stessa distribuzione con più di 400 variabile [9], [22].
L'algoritmo GSAT di base realizza una ricerca locale attraverso lo spazio degli assegnamenti dei valori di verità, cominciando con un assegnamento generato random, e poi ripetutamente modificando l’assegnamento di una variabile che minimizza il numero totale di clausole non soddisfatte. Come con alcuni problemi combinatoriali, i minimi locali nello spazio di ricerca sono problematici nelle applicazioni dei metodi di ricerca locale.
Un minimo locale è definito come uno stato il cui vicinato locale non include uno stato che è rigorosamente migliore. L’approccio standard nell’ottimizzazione combinatoriale nel terminare la ricerca quando è raggiunto un minimo locale [101] non funziona bene per la verifica della soddisfacibilità booleana, quanto tempo interessano solamente gli ottimi globali. In [116] è stato mostrato che continuando semplicemente a cercare facendo mosse laterali non migliorative, aumenta di molto la percentuale del successo dell'algoritmo [1].
La serie degli stati esplorati in sequenza attraverso mosse laterali nello spazio di ricerca sono chiamate altopiani. La ricerca attraverso gli altopiani domina spesso la ricerca GSAT. Per un’analisi dettagliata, si può vedere Gent e Walsh [35].
Il successo del GSAT è determinato dalla sua abilità di muoversi tra gli altopiani successivamente bassi. La ricerca fallisce se GSAT non può trovare modo di uscire dagli altopiani, sia perché tali transizioni dagli altopiani sono rare, sia perché sono inesistenti. Quando capita questo, si può semplicemente riavviare la ricerca con un nuovo assegnamento iniziale random.
Ci sono anche altri meccanismi per uscire dai minimi locali o altopiani che consistono nel fare occasionalmente mosse in salita. Da notare fra tali approcci l'utilizzo del simulated annealing [82], dove un parametro formale temperatura, controlla la probabilità che l'algoritmo di ricerca locale faccia una mossa in salita.
Nel 1993 Selman e Kautz [112] hanno proposto un altro meccanismo per introdurre questo tipo di mosse in salita. La strategia è basata sulla combinazione del random walk sulle variabili che appaiono nelle clausole non soddisfatte, con la ricerca locale greedy. La strategia può essere vista come un modo di introdurre del noise in una maniera molto focalizzata, perturbando solamente quelle variabili critiche alle clausole non soddisfatte rimanenti.
Selman
e al. hanno presentato dati sperimentali dettagliati che comparano le strategie
random walk, simulated annealing, random noise, e GSAT di base sulle formule
random computazionalmente difficili. Per ottenere le migliori performance per
ogni procedura hanno calibrato i valori dei vari parametri.
Hanno considerato particolarmente i problemi di pianificazione [77] e di sintesi dei circuiti [73], [75].
GSAT [116] effettua una ricerca locale greedy per assegnamenti soddisfacenti di una serie di clausole proposizionali [1.5.1], [1.5.2], [1.5.3]. La procedura comincia con un assegnamento di verità casuale. Poi si modifica l’assegnamento della variabile che minimizza il numero totale di clausole non soddisfatte. Da notare che il maggior decremento può essere zero (mosse laterali) o negativo (mosse in salita). I cambiamenti sono ripetuti fino quando viene trovato un assegnamento soddisfacente o si arriva al numero massimo di cambiamenti preimpostati MAXFLIPS. Questo processo, se necessario, è ripetuto fino a MAXTRIES volte.
In [116] è stato mostrato che GSAT migliora notevolmente in confronto alle procedure di ricerca backtracking, come la procedura DavisPutnam, su varie classi di formule, incluso le formule difficili generate random e le codifiche SAT di problemi Graph Coloring [69].
Come menzionato sopra, i minimi locali nello spazio di ricerca dei problemi combinatoriali sono i principali ostacoli nell’applicazione dei metodi di ricerca locale. L'utilizzo da parte del GSAT delle mosse laterali non elimina completamente questo problema, perché l'algoritmo può ancora bloccarsi sugli altopiani.
Perciò, è utile assumere dei meccanismi per uscire dai minimi locali o altopiani facendo mosse in salita (modifiche che aumentano il numero di clausole non soddisfatte). Vedremo in seguito due meccanismi per fare tali mosse [2].
Simulated annealing introduce le mosse in salita nella ricerca locale usando un modello noise basato sulla meccanica statistica [82]. Selman e al. hanno utilizzato l’algoritmo definito in Johnson e al. [77]: inizio con un assegnamento di verità generato random. Si sceglie ripetutamente una variabile random, e si calcola d, la modifica del numero di clausole non soddisfatte quando è modificata quella variabile. Se d £ 0 (mosse discendenti o laterali), si fa la modifica. Altrimenti, si modifica la variabile con probabilità e -d/T, dove T è un parametro formale chiamato temperatura. La temperatura potrebbe essere tenuta costante [3], oppure decrementata lentamente da una temperatura alta verso vicino zero secondo uno scheduling di raffreddamento. Spesso si utilizzano scheduling geometrici, nei quali la temperatura è diminuita ripetutamente moltiplicandola con un fattore costante < 1.
Dato uno scheduling di raffreddamento finito, simulated annealing non garantisce che trovi un ottimo globale, ovvero un assegnamento che soddisfa tutte le clausole. Perciò, Selman e al. nei loro esperimenti hanno utilizzato avvii random multipli, e calcolato il numero medio di riavvii R, necessari prima di trovare una soluzione.
L'algoritmo GSAT di base è molto simile all’annealing alla temperatura zero, ma differisce nel senso che GSAT impiega naturalmente riavvii e fa sempre una mossa in discesa se è disponibile. Il valore R per GSAT è semplicemente il numero medio di tentativi richiesti per trovare una soluzione.
Selman e Kautz [112] hanno presentato diverse estensioni della procedura GSAT di base. Una di queste estensioni combina la strategia di random walk con la ricerca locale greedy. Più precisamente, loro hanno proposto la seguente strategia random walk combinata:
· scegliere con probabilità p una variabile che si presenta in alcune clausole non soddisfatte e cambiare il suo assegnamento di verità.
· seguire con probabilità 1-p lo schema GSAT standard, facendo la migliore mossa locale possibile.
Notiamo
che le mosse walk possono
essere in salita.
Una versione più semplice della strategia random walk consiste nel non restringere la selezione della variabile scelta random, alla serie di variabili che appaiono nelle clausole non soddisfatte. Selman e al. hanno chiamato questa modifica random noise.
Si nota che random walk differisce sia dal simulated annealing che dal random noise, nel senso che le mosse in salita random walk sono collegate da vicino alle clausole non soddisfatte.
Selman e al. hanno comparato gli algoritmi GSAT di base, simulated annealing, random walk, e random noise su una serie di test, che includono sia i problemi CNF generati in modo random, che le codifiche booleane di altri problemi combinatoriali. I risultati sono mostrati nelle Tabelle 6.1, 6.2 e 6.3. Per ogni strategia sono dati il tempo medio in secondi impiegato per trovare un assegnamento soddisfacente [4], il numero medio di cambiamenti (flips) richiesto e il numero medio di riavvii R necessario prima di trovare una soluzione.
Per ogni strategia, Selman e al. hanno utilizzato almeno 100 riavvii random (il parametro MAXTRIES impostato in GSAT) per ogni istanza di problema; se sono stati necessari più di 20 riavvii prima di trovare una soluzione, la procedura è stata riavviata 1000 volte. Un “*” nelle tabelle, indica che non è stata trovata nessuna soluzione dopo più di 10 ore di funzionamento, o di aver riavviato più di 1000 volte la procedura.
I parametri per ogni metodo sono stati variati in un range di valori, e sono stati inclusi nelle tabelle solamente i risultati delle calibrazioni migliori. Selman e al. per il GSAT di base hanno variato anche i valori MAXFLIPS e MAXTRIES. Per il GSAT con random walk, gli autori hanno variato anche la probabilità p con cui è fatta una mossa non greedy, ed in modo simile per GSAT con random noise.
In tutti gli esperimenti di Selman e al., il valore ottimale di p è stato trovato tra 0.5 e 0.6. Per il simulated annealing con temperatura costante, gli autori hanno variato la temperatura T da 5 a 0 in passi da 0.05 (per T=5 le mosse in salita sono accettate con probabilità maggiore a 0.8).
Per le formule random, le performance migliori sono state trovate per T = 0.2. Le formule di pianificazione hanno richiesto una temperatura più alta T = 0.5, mentre la sintesi di circuiti booleani è stata risolta più rapidamente ad una temperatura bassa T = 0.15.
Gli autori hanno sperimentato anche con vari scheduling geometrici di raffreddamento, e non hanno trovato alcuno scheduling che sia meglio del miglior scheduling a temperatura costante.
Selman e al. non sono riusciti a migliorare significativamente il numero medio di riavvii necessario prima di trovare una soluzione con scheduling di raffreddamento molto lenti, nonostante l'effetto sul tempo d’esecuzione. Una spiegazione possibile per questo è che quasi tutto il lavoro per risolvere i problemi CNF consiste nel soddisfare poche delle ultime clausole non soddisfate. Questo corrisponde alla parte a bassa temperatura dello scheduling geometrico, dove la temperatura ha poche variazioni.
Le istanze random delle formule CNF sono spesso state utilizzate nella valutazione delle procedure di soddisfacibilità perché possono essere facilmente generate e manca qualsiasi struttura fondamentale nascosta, spesso presente nelle istanze fatte a mano. Sfortunatamente, a meno di grande cura nello specificare i parametri della distribuzione random, i problemi così creati possono essere banali da risolvere. Mitchell e al. [98] hanno mostrato come i problemi random computazionalmente difficili possono essere generati usando il modello con clausole di lunghezza fissa.

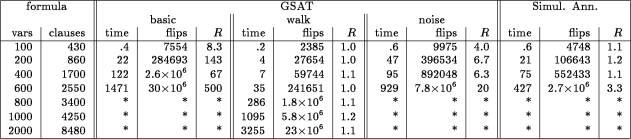
Tabella 6.1: Comparazione delle strategie noise su istanze 3CNF random difficili
Consideriamo che N sia il numero di
variabili, K
il numero di letterali per ogni clausola, e L
il numero di clausole. Ogni istanza è ottenuta generando L
clausole casuali, ognuna contenendo
![]() letterali. I K
letterali sono generati selezionando in modo random K
variabili, e ognuna delle variabili è negata con una probabilità di 50%.
La difficoltà di queste formule dipende in modo critico dal rapporto tra N
e L. Le formule più difficili sono
intorno alla regione dove le formule generate random hanno una possibilità
d’essere soddisfacibili di 50%. Per le formule 3CNF
(K=3)
gli esperimenti mostrano che questo è il caso per LZ4.3N.
Per N più grande, il rapporto critico per
il punto 50%
converge a 4.25. Selman e al.
hanno esaminato gli algoritmi intorno al punto 4.3
su formule con dimensioni comprese tra 100
a 2000
variabili; i risultati sono presentati nella Tabella 6.1.
letterali. I K
letterali sono generati selezionando in modo random K
variabili, e ognuna delle variabili è negata con una probabilità di 50%.
La difficoltà di queste formule dipende in modo critico dal rapporto tra N
e L. Le formule più difficili sono
intorno alla regione dove le formule generate random hanno una possibilità
d’essere soddisfacibili di 50%. Per le formule 3CNF
(K=3)
gli esperimenti mostrano che questo è il caso per LZ4.3N.
Per N più grande, il rapporto critico per
il punto 50%
converge a 4.25. Selman e al.
hanno esaminato gli algoritmi intorno al punto 4.3
su formule con dimensioni comprese tra 100
a 2000
variabili; i risultati sono presentati nella Tabella 6.1.
Per le formule più piccole (100 variabili), si osserva una piccola differenza nei run-times. Con l'aumento del numero delle variabili, la strategia random walk domina significativamente sugli altri approcci. Le strategie random noise e simulated annealing migliorano anche rispetto a GSAT di base, ma nessuno di questi metodi trova soluzioni per le tre formule più grandi [5]. Le performance del GSAT con walk sono notevoli, specialmente considerando il fatto che i più veloci metodi correnti di ricerca sistematica non possono risolvere le istanze 3CNF random con più di 400 variabili [22].
Le colonne marcate con flips danno il numero medio di cambiamenti richiesti per trovare un assegnamento. Nell’algoritmo simulated annealing un flips è un cambio attuale dell’assegnamento di verità. Comparando il numero di cambiamenti richiesti dalle varie strategie, si arriva alla stessa conclusione sulla relativa efficienza dei metodi.
Finalmente, viene considerato il numero medio di riavvii R necessari prima di trovare una soluzione.
GSAT di base si è facilmente bloccato sugli altopiani, e richiede molti riavvii random, in particolare per le formule più grandi. D'altra parte, GSAT con walk garantisce in sostanza di trovare un assegnamento soddisfacente. Combinando random walk con mosse greedy sulle variabili nelle clausole non soddisfatte, permette di uscire quasi sempre dagli altopiani che hanno pochi o nessun stato da cui può essere fatta una mossa in discesa. Anche le altre due strategie danno un valore migliorato di R rispetto al GSAT di base.
Selman e al. hanno considerato come un secondo esempio dell'efficacia delle varie strategie d’uscita, le codifiche dei problemi di pianificazione blocksworld [77]. L'analisi dei migliori assegnamenti trovati quando GSAT fallisce nel trovare un assegnamento soddisfacente, indica che le difficoltà sorgono dai minimi locali molto profondi. Per esempio, il problema di pianificazione conosciuto col nome di Hanoi corrisponde al puzzle familiare torri di Hanoi, che consiste nel muovere una pila di dischi tra tre pioli, non mettendo mai un disco più grande sopra uno più piccolo. Ci sono molti assegnamenti di verità che soddisfano quasi tutte le clausole che codificano questo problema, ma sono molto diversi dal corretto assegnamento soddisfacente; per esempio, un assegnamento simile può corrispondere a far slittare un disco fuori dal fondo della pila.
Dalla Tabella 6.2 si osserva che GSAT con random walk è nettamente superiore. Come in precedenza, GSAT di base non riesce a risolvere i problemi più grandi. GSAT con walk è approssimativamente 100 volte più veloce del simulated annealing sui due problemi più grandi, e più di 200 volte più veloce del random noise.

Figura 6.2: Comparazione delle strategie noise su codifiche SAT di problemi di pianificazione

Figura 6.3: Comparazione delle strategie di noise sui problemi di sintesi di circuiti come studiati da Kamath
Le strategie random noise e annealing su problemi grandi richiedono anche molti
più riavvii della strategia random walk prima di trovare una soluzione.
Kamath e al. [73] hanno sviluppato un set di codifiche SAT per i problemi di sintesi dei circuiti booleani per valutare una procedura di soddisfacibilità basata sulla programmazione di interi. Il compito da considerare era da ricavare un circuito logico partendo dal suo comportamento inputoutput. Selman et al. [116] hanno mostrato che GSAT di base è competitivo con il metodo di programmazione di interi. Nella Tabella 6.3 sono mostrati i risultati sperimentali di Selman e al. sulle cinque più difficili istanze considerate da Kamath. Dalla tabella si nota che le entrambe strategie random walk e simulated annealing migliorano in modo significativo in confronto a GSAT, con random walk che qualche volta funziona meglio di simulated annealing. Per fare dei paragoni, Selman e al. hanno incluso anche i tempi originali riportati da Kamath e al [6]. In questo caso, la strategia di random noise non porta ad un miglioramento sul GSAT di base. Infatti, il mixing nel random noise sembra peggiorare le performance del GSAT.
Gli esempi di Kamath e al. [73] sono stati ricavati dai circuiti booleani collegati in modo casuale. Quindi, anche se le codifiche di SAT contengono alcune strutture intricate di porte booleane, c'è ancora un aspetto casuale delle istanze del problema. In seguito, Kamath e al. [75] hanno generalizzato il loro approccio, per considerare i circuiti con uscite multiple. Utilizzando questa formulazione, si possono codificare i circuiti booleani utili nelle applicazioni pratiche. Alcuni esempi sono i circuiti del sommatore e del comparatore. Selman e al. hanno codificato il comportamento I/O di molti di questi circuiti e utilizzato GSAT con walk per risolverli.
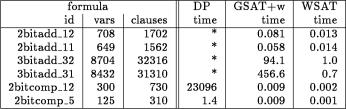
Figura 6.4: Confronto del metodo completo DP con le strategie di ricerca locale su problemi di sintesi di circuiti (tempi in secondi)
La Tabella 6.4 mostra i risultati di Selman e al. GSAT+w significa GSAT con walk, p=0.5. Il tipo di circuito e indicato nella tabella. Per esempio, ogni assegnamento soddisfacente per la formula 2bitadd_11 corrisponde ad un progetto per un sommatore a 2bit che usa un PLA (Programmable Logic Array). Il suffisso 11 indica che il circuito è costretto ad utilizzare solamente 11 porte AND. Si vedrà dalla tabella che GSAT con walk può risolvere le istanze in tempi che vanno da meno di un secondo ad alcuni minuti.
Selman e al. hanno incluso anche i tempi per la procedura DavisPutnam, includendo anche una versione di questa procedura sviluppata da Crawford e Auton [15]. Al momento rispettivo questa procedura era uno dei metodi completi più veloci, ma è sorprendente vedere che risolve solamente due degli esempi [7]. Con “*” è stato indicato che il metodo ha girato per 10 ore senza trovare un assegnamento. Le buone performance del GSAT con walk su questi problemi indicano che i metodi di ricerca locale possono lavorare bene su problemi strutturati che non contengono alcun componente casuale.
Larrabee [86] aveva proposto una traduzione del problema della generazione di campioni di test per i circuiti VLSI in un problema SAT. Selman e al. hanno comparato le performance del GSAT con walk e quello del DP su molte delle formule di Larrabee. I loro risultati sono mostrati nella Tabella 6.5.
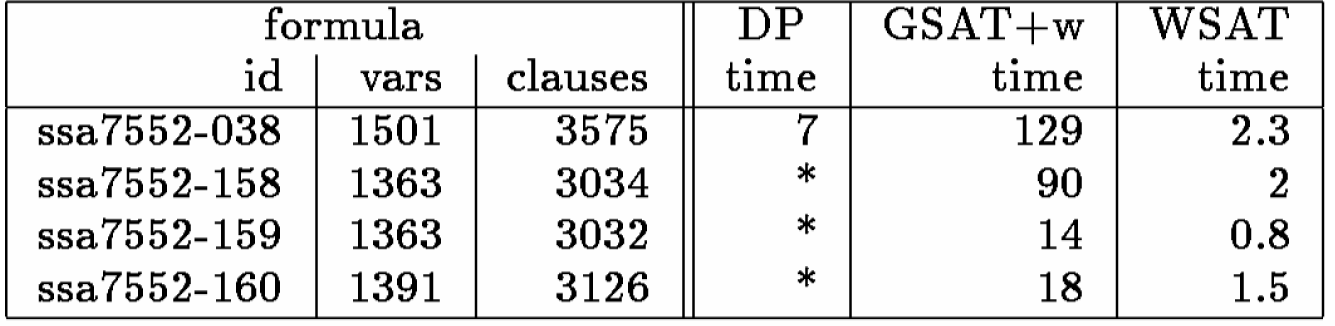
Figura
6.5: Confronto del DP con le strategie di ricerca locale su problemi di
diagnosi di circuiti da Larabee (tempi in secondi)
Si nota che il GSAT con walk gira nuovamente molto bene, specialmente se comparato alla ricerca sistematica DP. Questi risultati e quelli per la sintesi dei circuiti presentano particolare interesse perché riguardano le codifiche dei problemi con chiara applicazione pratica.
Selman e al. hanno implementato un algoritmo che perfeziona la strategia random walk del GSAT con semplici ma significative modifiche. Questo algoritmo, chiamato WSAT (walksat), fa cambiamenti, scegliendo per prima in modo random una clausola che non è soddisfatta dal corrente assegnamento, e poi scegliendo (sia a caso che secondo un’euristica greedy) una variabile nella clausola da modificare. Così, mentre GSAT con walk può essere visto come aggiungere walk ad un algoritmo greedy, WSAT può essere visto come aggiungere golosità come euristica al random walk. Sembra dipendere da particolari classi di problemi il fatto che WSAT migliori o no rispetto al GSAT con walk.
Un'inaspettata e interessante osservazione degli autori è che potrebbe essere una grande discrepanza tra il funzionamento del GSAT con 100% walk (p=1.0) e il funzionamento del WSAT, dove le variabili sono scelte a caso in una clausola non soddisfatta. Ad un primo sguardo, queste scelte sembrerebbero essere identiche. GSAT mantiene una lista (senza duplicati) delle variabili che appaiono nelle clausole non soddisfatte, e sceglie a caso da quella lista; così, ogni variabile che appare in una clausola non soddisfatta è scelta con uguale probabilità. WSAT utilizza un processo casuale a due passi come descritto sopra (scegliendo prima una clausola, e poi una variabile), che favorisce le variabili che appaiono in molte clausole non soddisfatte. Per molte classi di formule, la differenza sembra non essere significativa. Comunque, GSAT con 100% walk non risolve i problemi di diagnosi dei circuiti, mentre WSAT con scelta random può risolverli tutti.
Selman e al. hanno comparato le performance del GSAT con walk ai metodi studiati da Hansen e Jaumard [57] per MAXSAT. I loro risultati appaiono nella Tabella 6.6.
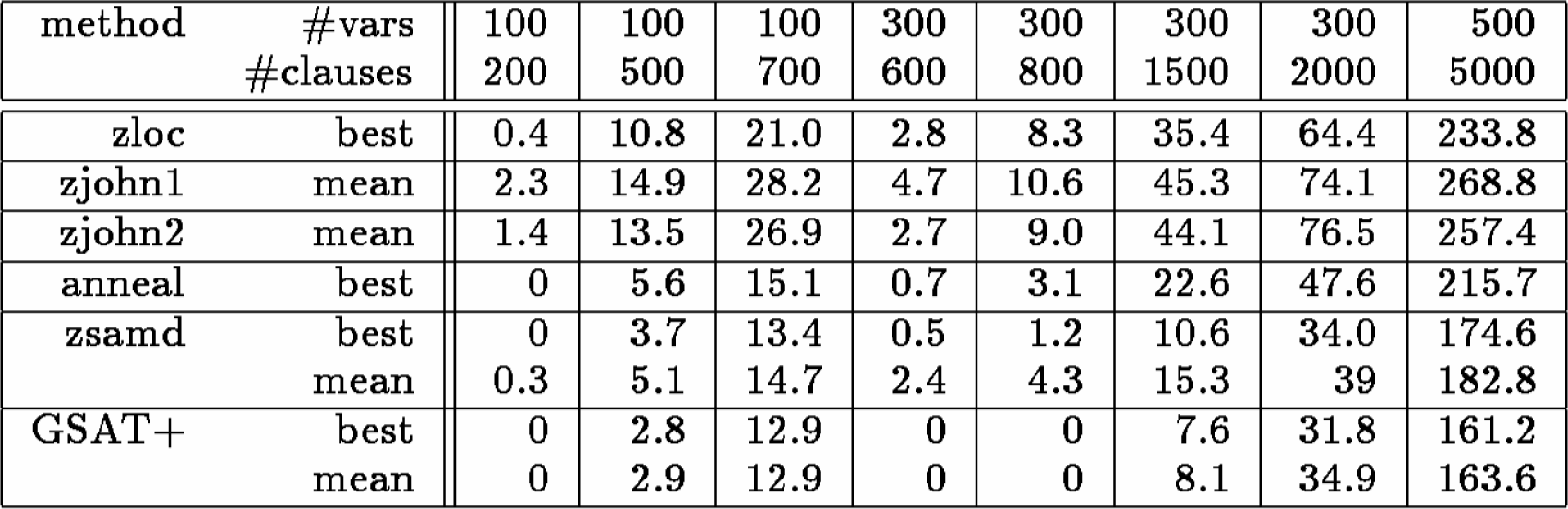
Figura
6.6: Risultati sperimentali per MAX-3SAT. I dati per i primi cinque metodi
sono da Hansen e Jaumard.
Hansen e Jaumard hanno analizzato cinque algoritmi diversi per MAXSAT, un algoritmo di ricerca locale base chiamato zloc, due algoritmi deterministici proposti da David Johnson [69 ] chiamato zjohn1 e zjohn2, un approccio simulated annealing chiamato anneal, e il loro algoritmo “steepest ascent, mildest descent” “zsamd”. L'ultimo è simile al GSAT di base con una forma di lista tabu [50 ].
Selman e al. hanno ripetuto i loro esperimenti che utilizzavano GSAT con walk. Le istanze dei problemi sono istanze 3SAT generate random. Per ogni dimensione del problema, sono stati generati in modo random 50 problemi, ed ogni problema è stato risolto 100 volte, utilizzando diversi assegnamenti iniziali random. Selman e al. hanno incluso nella tabella i valori dei numeri migliori e medi delle clausole non soddisfatte trovato durante le 100 prove. Per esempio, nelle istanze 3SAT con 500 variabile - 5000 clausole, i migliori assegnamenti trovati del GSAT con walk contenevano una media di 161.2 clausole non soddisfatte. Come possiamo notare dalla tabella, GSAT con walk ha trovato costantemente soluzioni migliori rispetto a qualsiasi altro metodo. Notiamo che c'è solamente una piccola differenza tra i valori migliori e quelli medi trovati dal GSAT con walk, indicazione che i valori migliori sono, infatti, vicini ad ottimo.
[1] Minton ed al. (1990) hanno incontrato un fenomeno simile nella loro applicazione di ricerca locale nel risolvere problemi grandi di scheduling.
[2] se l’unica mossa possibile per il GSAT è ascendente, esso farà tale mossa, ma tale mossa obbligata in salita è molto rara, e non è efficace per uscire dai minimi locali.
[3] questa forma di annealing corrisponde all'algoritmo di Metropoli (Jerrum 1992).
[4] gli algoritmi sono stati implementati in C e girano su un SGI Challenge con un processore MIPS R4400 a 70 MHz.
[5] GSAT con walk trova essere soddisfacibili approssimativamente 50% delle formule nella regione difficile, come si sarebbe aspettato al punto di transizione per SAT.
[6]
la procedura di soddisfacibilità di Kamath ed al. girava su una VAX 8700
con il codice scritto in FORTRAN e C.
[7] esperimenti preliminari indicano che alcune di queste formule possono essere risolte anche combinando DP con avvii multipli che casualmente permutano le variabili. Dettagli appariranno nella versione intera.
| Indietro | ||
| Applicazioni |
SAT solver |
Relsat |