Il programma di pianificazione Ipp offre numerose opzioni per poter
ottimizzare la ricerca della soluzione di un problema di pianificazione.
Ipp viene distribuito in rete fornendo le sorgenti in ANSI C e quindi può
essere facilmente modificato per sperimentare nuove tecniche basate sulla
pianificazione mediante planning Graph. Nella versione modificata al Dipartimento
dell'Elettronica per l'Automazione viene applicata ed estesa un'idea di
Carla P. Gomes che prevede di controllare il numero di backtracks effettuati
durante la ricerca della soluzione. Il controllo sui backtracks viene usato
al fine di stabilirne un numero massimo (chiamato Cut_off), dopo il quale
ritornare al nodo di partenza dell'albero di ricerca, effettuare un'operazione
di "randomize", cioè mescolare casualmente gli archi fra i nodi
dell'albero (poiché Ipp utilizza proprio questo ordinamento per
definire la zona dello spazio di ricerca da esaminare) e ricominciare la
ricerca. In questo modo ogni volta che viene eseguita questa operazione
la ricerca riparte seguendo rami diversi da quelli di esaminati precedentemente.
Così si riesce ad evitare che rami dell'albero di ricerca senza
soluzioni vengano analizzati troppo a fondo, sciupando tempo utile per
trovare la soluzione. In questa versione modificata di IPP(chiamata
GPP) il numero di backtracks viene incrementato ogni volta che viene
fatta una memoizzazione, quando, cioè, il programma trova che un
insieme di sottogoal ad un dato livello non è realizzabili ossia
mutuamente esclusivi. GPP memorizza questo insieme di fatti così
ogni volta che lo incontra evita di rianalizzarli perché sa già
che essi porteranno sicuramente a sottogoal irrealizzabili. In seguito
a prove eseguite con questa tecnica sono stati ottenuti grafici e tabelle
relativi ai tempi di ricerca della soluzione impiegati da Ipp Standard
e dalla prima variante con il Cut_off; i grafici mostrano chiaramente che
questa variante garantisce tempi di ricerca della soluzione sempre inferiori
o uguali rispetto a quelli ottenuti da Ipp con il paramentro Cut_off C=0
(cioè Ipp che funziona nella versione standard). Questo risultato
è senz'altro incoraggiante perché il Cut_off può così
essere utilizzato senza paura di peggiorare le prestazioni del pianificatore
e pensando che in molti casi le migliorerà. Una seconda considerazione
riguarda il valore da assegnare al Cut_off prima di ogni ricerca. Dai grafici
si capisce subito che il tempo di ricerca della soluzione non è
strettamente dipendente dal valore di C specificato, a meno di non utilizzare
numeri troppo altri o troppo bassi. In questi casi, infatti, il pianificatore
tende a lavorare in una configurazione simile a quella standard (se C è
alto), oppure a utilizzare troppo tempo per eseguire tantissime operazione
di randomize (se C è basso), compromettendo i tempi di ricerca.
Da queste considerazione si può pensare di fissare un valore di
default per il Cut_off a C=10000 sicuri di non cadere nelle 2 zone di decadimento
delle prestazioni per ogni tipo di problema. Un passo avanti consiste nel
fissare altri 2 limiti al numero di backtracks totali per "spendere" meno
tempo in grafi dove non esiste soluzione o dove per trovarla bisognerebbe
analizzare a fondo tutto il grafo. Questa operazione viene fatta per espandere
il planning graph di un livello ulteriore, applicando una volta ancora
gli operatori del problema, in modo da aumentare il numero di soluzioni
possibili. Il primo limite, chiamato init_step_cut, indica dopo quanti
backtracks effettuare la prima espansione di livello; il secondo, step_cut,
indica l'incremento del numero di backtracks dopo i quali effettuare le
successive, ed eventuali, espansioni di livello e viene moltiplicato per
2 ogni volta che si raggiunge il numero di backtracks specificato in Init_step_cut.
In ogni caso quando viene effettuata una espansione di livello la ricerca
comincia da capo. Con questa idea si espande il numero di soluzioni possibili,
tra le quali poi deve essere effettuata la ricerca di quella accettabile,
a costo di un aumento del numero di livelli che saranno presenti nel piano
soluzione da eseguire per andare dalla situazione iniziale ai goal. Generalmente
risultati accettabili si possono ottenere in domini in cui ogni espansione
di livello comporta un grande aumento delle soluzioni, tanto grande da
poter sopperire alla perdita di tempo dovuta alle varie operazioni di randomize
ed espansione di livello. Il metodo delle espansioni di livello è
stato usato congiuntamente al randomize perché da solo non
riesce a migliorare l`efficienza temporale della ricerca. Se, infatti,
durante la ricerca viene raggiunto il numero di backtracks specificato
da Init_Step_Cut, questa fase viene interrotta e si procede
ad una espansione di livello. Il nuovo Planning Graph è così
costituito da un ulteriore livello dei fatti e delle azioni e ciò
determina uno spazio di ricerca notevolmente ampliato. Viene quindi riavviata
la fase di ricerca di IPP, che applica all'ultimo livello t
le azioni NO-OP per realizzare i goal G. In questo modo si ottengono
i sottogoal del livello t-1 che sono identici a G stesso
poiché gli effetti additivi e le precondizioni delle NO-OP coincidono.
Il sistema di pianificazione considererà ora un Planning Graph di
t-1 livelli (cioè come quello considerato prima dell'ultima
espansione) e quindi ripeterà tutte le scelte effettuate nella fase
di ricerca precedente all'espansione. In pratica espandendo il Planning
Graph, IPP in ogni caso deve completare il processo di ricerca precedentemente
interrotto (per il superamento del numero D di backtrack) prima
di poter effettuare nuove scelte anche se non verranno riesaminate le porzioni
dello spazio di ricerca precedentemente 'memorizzate'. Si capisce quindi
che non ha senso espandere il livello se in ogni caso il pianificatore
deve terminare il processo di ricerca appena interrotto, anche perché
l'espansione richiede un certo tempo non utilizzato dalla fase di ricerca.
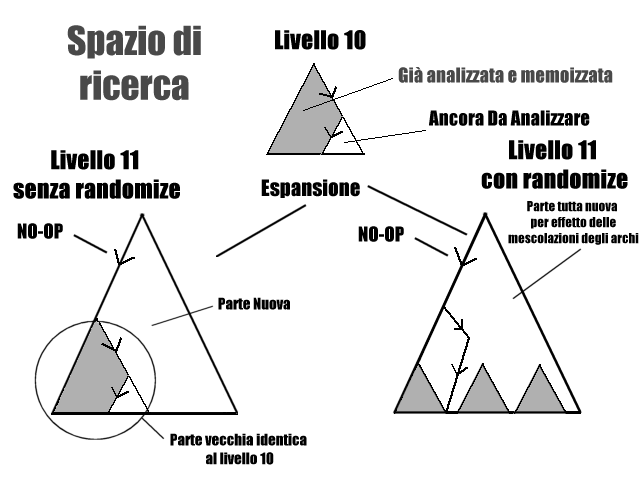
Invece utilizzando anche la tecnica del randomize ogni volta che
c'è un'espansione gli archi del Planning Graph vengono mescolati
casualmente e quindi il nuovo cammino nello spazio di ricerca risulterà
diverso da quello precedente (vedi la figura) con la conseguente analisi
di nuove zone.
 ' '
Sono state esaminate quindi varie configurazioni di questi parametri
al fine di definire dei valori di default applicabili nei vari domini per
ottimizzare le prestazioni temporali della ricerca. Per specificare i 3
valori sono stati introdotti a Ipp originale 3 nuovi parametri d'ingresso
C D E rispettivamente per Cut_off, Init_step_cut e Step_cut . Successivamente
sono stati creati dei files della Shell di Unix per poter lanciare ricorsivamente
Ipp con diversi valori C D E. Il programma è stato fatto girare
su piattaforma Linux su un PII 333Mhz con 64Mbyte di Ram e 128 Mbyte di
Swap su disco, con i 4 problemi diversi: rocket_a, rocket_b, logistic_a,
logistic_b. Le prove effettuate si sono orientate in 2 direzioni: primo
confrontare i tempi ottenuti da IPP in ricerca sistematica, cioè
senza specificare C D E, con quelli ottenuti usando il valore C di Cut_off,
secondo aggiungendo ai confronti anche i tempi con C D E specificati. I
risultati ottenuti sono stati senz'altro incoraggianti, infatti anche specificando
valori non ottimali di C D E i tempi erano più bassi (dalle 5 alle
10 volte) della ricerca sistematica, e usando valori ottimi per i 3 parametri
si ottenevano soluzioni in tempi dalle 20 alle 50 volte migliori. Una volta
trovate delle coppie di valori D E ottimi per i nostri domini abbiamo eseguito
delle ricerche tenendo fissi questi valori e variando in maniera molto
fine i valori di C per vedere come quest'ultimo influiva sul tempo finale.
Abbiamo così capito che a meno di non prendere C molto piccoli o
molto grandi (cioè con Ipp esegue tantissimi o pochissimi randomize)
il suo valore non influiva sulle prestazioni della ricerca come D ed E.
Nonostante questo, però, abbiamo rilevato valori di C che riducono
i tempi della ricerca rispetto ad altri. L'analisi dei dati ottenuti indica
una certa regolarità nella distribuzione dei tempi rispetto ai valori
di D ed E. In particolare è molto significativo il valore di E perché
fornisce un'indicazione su quante espansioni di livello verranno fatte.
Un valore grande di E causerà poche espansioni, mentre uno piccolo
ne causerà molte. Il valore di D ha un'importanza minore ma comunque
fondamentale perché mi dice dopo quanti backtracks cominciare le
espansioni. Un valore troppo alto di D potrebbe dar luogo a poche (o nessuna)
espansioni e concedere molto tempo di ricerca nel primo livello della soluzione.
Un D basso fa cominciare subito l'espansione garantendo un immediato aumento
delle soluzioni possibili, ma negando la possibilità di trovare
la soluzione nel livello più basso possibile per il problema in
analisi. Comunque in generale le zone di maggior importanza, cioè
con tempi sensibilmente più bassi rispetto alla ricerca col solo
C indicato, sono quelle con D ed E bassi. Da queste considerazioni abbiamo
fissato come ottime coppie D E del tipo (500,100), (1000,100), (2000,100)
e le abbiamo usate per la ricerca "fine" dei valori ottimi per C. Per valori
alti di C, dove Ipp esegue pochissimi (o nessun) randomize con relativo
ritorno a capo, ci si avvicina molto al caso della ricerca sistematica
di Ipp e quindi non si sentono molto gli effetti dell'utilizzo del Cut_off.
Come accennato prima, i valori di C ottimi sono quelli medi e continuando
a diminuire C arriviamo alla situazione in cui il pianificatore consuma
più tempo per eseguire le operazioni relative al Cut_off che per
cercare veramente la soluzione del problema, facendo registrare un degrado
delle prestazioni.
Per riassumere è importante notare che valori di D ed E bassi
portano ad un numero elevato di espansioni di livello e alla conseguente
riduzione del tempo di ricerca nell'albero tra una espansione e l'altra.
In questo modo aumentano molto le soluzioni presenti nello spazio di ricerca
e quindi anche la probabilità di trovarle in un tempo contenuto.
Nei domini dove l'aumento di soluzioni ad ogni espansione è notevole
questa versione di Ipp presenta ottime prestazioni anche se ci sono 2 effetti
collaterali da tener presenti; primo l'aumento dello spazio di ricerca
si può tradurre in un notevole incremento di utilizzo di memoria
da parte del programma, secondo, la soluzione trovata dal pianificatore
non è più ottima, cioè non si riesce a raggiungere
lo stato Goal con il numero minimo di livelli possibile, ma, generalmente
con molti di più. Partendo sempre dall'idea dell'espansione di livello
abbiamo provato a modificare la relazione che c'era fra il numero di bakctracks
totali, il valore di Cut_off e quando fare le espansioni di livello. Alla
base di questo cambiamento c'era l'idea di far espandere molte volte il
livello all'inizio della ricerca, quando ci sono poche soluzioni e poi
ridurre le espansioni per lasciare più tempo al pianificatore di
cercare nello spazio di ricerca più ampio e con più soluzioni.
Così si perdeva poco tempo a cercare soluzioni all'inizio quando
sono molto poche e quindi è bassa la probabilità di trovarle
e lasciare molto spazio alla ricerca quando le soluzioni sono molte. Al
posto dei 3 parametri Cut_off, Init_step_cut e Step_cut sono stai messi
i nuovi Cut_off, Restart, Multiplier. Il funzionamento di Cut_off è
simile al precedente, però, adesso il suo valore viene moltiplicato
per il Multiplier ogni volta che viene fatta un espansione di livello e
la specifica di quest'ultimo viene lasciata a libero arbitrio dell'utente
di Ipp in modo che esso possa valutare quali casi siano migliori di altri.
L'altra importante evoluzione riguarda l'espansione di livello che questa
volta è regolata da Restart; esso indica il numero di "randomize"
(ritorno a capo), che il programma fa ogni volta che il numero di backtracks
supera il valore Cut_off, dopo il quale eseguire l'espansione al livello
e calcolarne il nuovo Cut_off, moltiplicando quello attuale per il Multiplier
. In pratica in questo modo indico al pianificatore quanto tempo cercare
la soluzione in un livello prima di espanderlo, tempo che dipende strettamente
da numero indicato con Restart e Cut_off. Con questa tecnica si riesce
a controllare meglio, rispetto a quella precedente, dove indirizzare la
ricerca della soluzione, dove concedere molto tempo al pianificatore per
trovarla e dove no. Mantenendo un valore basso di Restart si ottengono
molte espansioni di livello e quindi, in genere, miglioramenti in termini
temporali, proprio come con valori di Init_step_cut e Step_cut bassi. Al
contrario valori alti di Restart concedono molto tempo di ricerca in ogni
livello privilegiando soluzioni con un basso numero di azioni ma penalizzando
il tempo per trovarle. Queste considerazioni vengono ulteriormente raffinate
considerando che anche Cut_off e Multiplier svolgono un'azione simile.
Quindi con questi 3 parametri posso scegliere meglio, che con quelli della
precedente tecnica, come e dove indirizzare la ricerca anche se bisogna
valutare molto più attentamente rispetto a prima, la scelta dei
loro valori. E' importante segnalare che questi ultimi test, nonostante
siano stati eseguiti con un PII 450 e 256Mbyte di Ram, indicano che il
metodo offre certamente un'efficienza, in termini di tempo di ricerca della
soluzione, inferiore rispetto al primo usato. Se, però, confrontiamo
questi risultati con quelli ottenuti con la ricerca sistematica di Ipp,
essi denotano un miglioramento temporale in alcuni casi anche notevole.
Un vantaggio di questa variante del pianificatore e che permette di trovare
il piano soluzione con un numero di livelli minore rispetto a prima e quindi
in generale con meno azioni da eseguire. Specificando adeguatamente in
valori C D E si può decidere di privilegiare questo aspetto oppure
la velocità di ricerca della soluzione. Quindi quest'ultima variante
può essere considerata un caso intermedio fra Ipp standard, che
trova un piano soluzione "minimo" ma in un tempo alto, e la versione del
pianificatore con l'espansione di livello regolata da Step_cut e Init_step_cut,
che seppur con un numero elevato di livelli del piano Goal, offriva tempi
di ricerca molto contenuti. Un suggerimento per delle future sperimentazioni
consiste nel valutare, con adeguati indicatori, la dimensione del Planning
Graph e le relazioni di mutua esclusione presenti in esso, e in base a
queste considerazioni fissare valori di Cut_off, Restart e Multiplier se
non ottimi che almeno non risultino peggiorare le prestazioni di Ipp standard
in tutti i casi e che in alcuni siano in grado di migliorare notevolmente
il tempo di ricerca della soluzione. Per riassumere, se si è interessati
unicamente a minimizzare i tempi di ricerca della soluzione di un problema,
senza voler controllare efficacemente il numero di livelli, allora è
meglio usare la tecnica con Cut_off, Init_step_cut e Step_cut. Se invece
si preferisce privilegiare quest'ultimo aspetto o tutti e 2 contemporaneamente
è meglio usare il metodo di Cut_off, Restart e Multiplier a costo
però di dover porre maggior attenzione nella scelta dei loro valori.
Infatti per questa tecnica in particolare è difficile individuare
dei valori di default perché ogni dominio e ogni problema ne richiederebbe
di diversi. Nella realtà, comunque, ogni azione ha un costo, in
termini temporali o di risorse, e quindi una soluzione con molti livelli
ma trovata in poco tempo può essere peggiore di una con pochi livelli
ma fornita più tardi. |
 '
'