|
|
| TEORIA |
Uno dei grossi problemi di cui si occupa la disciplina dell'intelligenza
artificiale è la pianificazione cioè individuare un insieme
di azioni da eseguire in specifici istanti temporali per andare da uno
stato iniziale
I ad uno finale detto Goal G utilizzando un
insieme di operatori
O. Sono disponibili in rete diversi tipi di
pianificatori ognuno con caratteristiche diverse: UC-POP, SATPLAN, PRODIGY,
BLACKBOX, GRAPHPLAN, ecc. L'efficacia di questi pianificatori si misura
secondo importanti fattori come: completezza, correttezza, individuazione
di una soluzione ottima, terminazione su problemi non risolvibili ed efficienza.
Noi ci occuperemo di un'estensione di GRAPHPLAN chiamata IPP o IP²,
che, integrando agli operatori STRIPS caratteristiche tipiche di
ADL,
aumenta l'espressività del vecchio pianificatore. Queste estensioni
riguardano la possibilità di usare effetti con quantificatori universali
e condizionali che GRAPHPLAN, basato su STRIPS, non aveva.Vediamo ora di
preciso come si opera in Ipp per formalizzare e risolvere un problema di
pianificazione P
solitamente espresso mediante una quadrupla (D,I,G,O).
Per prima
cosa bisogna identificare un dominio D del problema, cioè
un insieme finito d'oggetti che definiscono una certa porzione del mondo
reale che si vuole analizzare. Ora si deve specificare la situazione iniziale
I
nella quale si trova il mondo all'istante iniziale per pianificare una
sequenza di azioni atta al raggiungimento della situazione finale o goal
G.
Sia I che G sono definiti tramite un insieme di formule atomiche
che rappresentano, in un certo istante di tempo, i fatti veri nel dominio
D
in cui mi sono posto.Viene inoltre specificato un insieme di operatori
O
che indica al pianificatore quali azioni possono essere eseguite a partire
dai fatti iniziale per arrivare ai fatti Goal. Formalmente un operatore
consiste in una quadrupla così composta: nome, lista delle variabili
usate, precondizioni (in forma di formule atomiche), effetti che a loro
volta possono essere condizionali, additivi o di cancellazione. Un operatore
le cui variabili sono istanziate ad uno specifico istante temporale è
un azione. Un azione, per essere usata, richiede che le sue precondizioni
siano vere in un certo istante di tempo e, solo in questo caso, gli effetti
additivi rendono verinuovi fatti
del problema mentre quelli cancellanti negano fatti già presenti.
Esiste inoltre un operatore predefinito NO-OP necessario per propagare
il valore di verità di un fatto nel tempo. Per ogni fatto fl'unica
precondizione di NO-OP_f è f stesso e l'unico effetto
è ancora f. Una volta specificato P
non resta che fornirlo al programma di pianificazione scelto e attendere
l'insieme ordinato delle azioni da eseguire per andare dalla situazione
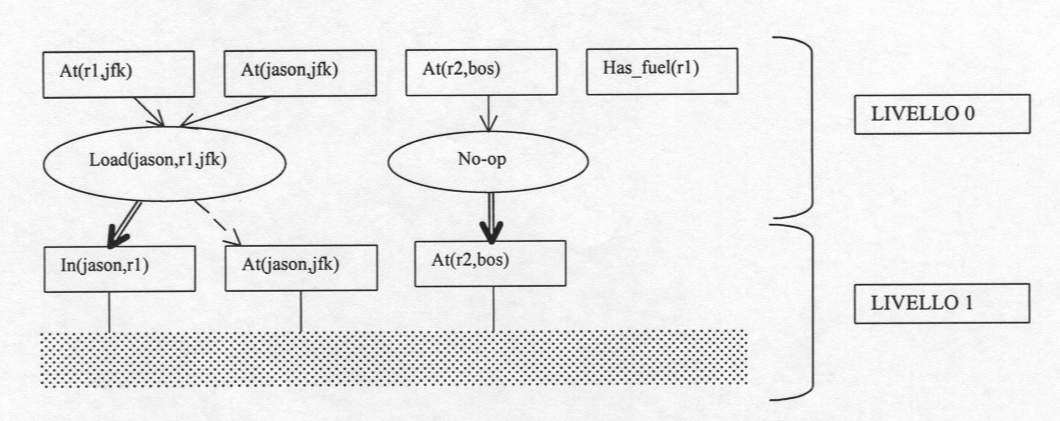
iniziale I a quella goal G.Nella figura sottostante i fatti
vengono rappresentati con dei quadrati e gli operatori con delle ellissi.
I fatti che soddisfano le precondizioni di un operatore sono collegati
ad esso attraverso archi semplici, quelli che sono generati additivamente
con archi doppi e quelli di cancellazione con archi a linee tratteggiate.
Questa notazione è la stessa usata dal programma di visualizzazione
XGV
(Vedi Appendice B per il link).Il programma costruisce un grafo
diretto aciclico a livelli, detto Planning graph, formato da due
insiemi di nodi N=Nf È NodoveNoeNfcorrispondono
rispettivamente l'insieme delle azioni e l'insieme dei fatti. Questi sono
collegati fra loro da un'insieme di archi E
formato dagli archi delle precondizioni Ep
(che vanno da un elemento diNf
a uno di No), da
quelli dei fatti additivi Ea
e da quelli cancellanti Ed (entrambi
da No a Nf ).
In ogni grafo ( che deve iniziare e finire con un livello fatti ) azioni
e fatti sono organizzati in livelli alterni e numerati. Il primo livello
fatti (livello 0) contiene tutti i fatti specificati come situazione iniziale
e una riga sotto ad essi c'è il primo livello azioni(livello 0)
che contiene tutti gli operatori applicabili dati l'insieme dei fatti iniziali.
A questo punto devo costruire il livello numero 1 applicando ai fatti del
livello 0 gli operatori eseguibili. In pratica per ogni operatore devo
vedere se i nodi precondizione sono presenti nel livello precedente e,
in tal caso, generare gli effetti additivi e di cancellazione che l'operatore
stesso prevede. In questo modo nel livello 1 vengono ad esserci tutti i
fatti del livello 0 (propagati dal NO-OP) e quelli nuovi generati
dagli effetti additivi e cancellanti degli altri operatori usati.
 Durante la fase di costruzione del Planning Graph vengono inoltre definite le relazioni di mutua esclusione tra coppie di azioni e coppie di fatti. Tali relazioni risultano fondamentali nella successiva fase di ricerca. Il concetto di mutua esclusione segue direttamente quello di Interferenza e di Competing needs (precondizioni contrastanti). Due azione interferiscono fra loro se una cancella anche una sola precondizione o un effetto additivo di un'altra. Due azioni hanno competing needs se i fatti delle loro precondizioni sono mutuamente esclusivi, cioè se non è possbile rendere veri entrambi i fatti allo stesso istante temporale. Due azioni sono dunque mutuamente esclusive se ad un certe istante temporale interferiscono fra loro o hanno competing needs. Due fatti sono mutualente esclusivi se nessuno stato del mondo può renderli veri entrambi contemporaneamente. Per concludere, un operatore è applicabile ad un livello dei fatti Nf(n) se e solo se in questo livello le sue precondizioni sono presenti e non mutuamente esclusive. In questo modo il pianificatore non aggiunge al grafo potenziali conflitti fra azioni o fatti.Questo procedimento viene ripetuto n volte fino che i goal G non appartengono all'istante finale e non sono mutuamente esclusivi (in tal caso viene avviato il processo di ricerca) oppure finché il grafo non è stabilizzato e l'ultimo livello contiene una coppia di elementi di G mutuamente esclusivi (il problema non ha soluzione). Un grafo si dice stabilizzato al livello n se il numero di fatti presenti (|Nf(n)|=|Nf(n-1)|)e di coppie di fatti mutuamente esclusivi in n è uguale a quelli del livello precedente n-1. Quindi un problema di pianificazione P non ha soluzione se il suo Planning Graph è stabilizzato a n e, le formule atomiche del Goal non sono contenute nel livello fatti n (Nf(n) ) o due formule atomiche dei Goal sono mutuamente esclusive. In caso contrario la costruzione grafo si ferma e comincia la ricerca, a partire dal Goal fino ai fatti iniziali. Il pianificatore infatti parte dall'ultimo livello fatti Nf(n) raggiunto durante la costruzione del grafo e cerca le azioni del livello n-1 che supportano i goal in Nf(n). Come passo successivo Ipp calcola i fatti goaldel livello n-1 basandosi sulle precondizioni delle azioni trovate precedentemente. Graficamente il pianificatore sceglie gli archi che vanno dai fatti goal di Nf(n) fino ai loro operatori in No(n-1) e poi definisce, tramite le precondizioni di questi, i sottogoal del livello Nf(n-1). Questo spostamento lungo gli archi non è univoco, infatti più di un operatore può portare a un fatto goal e quindi l'algoritmo di ricerca sceglie di volta in volta uno fra gli archi disponibili. Se l'insieme sottogoal contiene fatti mutuamente esclusivi, il pianificatore fa backtrack, torna indietro, e sceglie altri archi diversi da quelli di prima. Viene fatto così un successivo controllo sull'insieme delle azioni scelte per vedere se è minimo cioè se ogni azione rende supportato un fatto goal che non è reso vero da nessun altra azione dell'insieme stesso. Se ciò non è verificato Ipp fa backtrack e viene valutato un nuovo insieme di azioni e archi. Le precondizioni delle azioni valide definiscono il nuovo insieme di goal del livello Nf(n-1) e la ricerca prosegue in questo livello sempre cercando nuove strade quando i controlli fatti danno esito negativo. Se si riesce ad arrivare ai fatti della situazione iniziale significa che la ricerca ha avuto successo e il piano soluzione per il mio problema di pianificazione P consiste nell'insieme di azioni che Ipp ha selezionato (e non scartato) nella sua salita fra i livelli. Se il pianificatore necessita di fare backtrack al massimo livello del grafo (cioè quello dei goal) significa che non è possibile trovare soluzione per il problema P. Allora il Planning Graph viene esteso con un livello aggiuntivo di azioni e di fatti e ricomincia la ricerca con questo nuovo grafo. Questo processo di espansione e ricerca termina o quando viene trovata una soluzione o se il problema risulta essere irrisolvibile. |
![]()