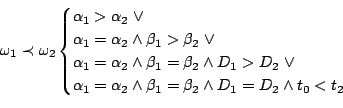Next: Individuazione delle possibili soluzioni
Up: MMA: gestione delle riunioni
Previous: MMA: gestione delle riunioni
Prima di identificare le possibili soluzioni il gestore delle riunioni esamina le risposte delle agende invitate e costruisce le funzioni obiettivo che permetteranno di valutare la qualità degli intervalli individuati. Tali funzioni vengono utilizzate anche per la selezione di un sottoinsieme delle possibili soluzioni, allo scopo di limitarne il numero (che altrimenti potrebbe essere infinito) ed evitare di considerare soluzioni di scarsa rilevanza.
Per ogni utente 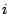 invitato alla riunione vengono costruite, sulla base della risposta ricevuta dal suo UPA, due funzioni, che chiamiamo disponibilità (
invitato alla riunione vengono costruite, sulla base della risposta ricevuta dal suo UPA, due funzioni, che chiamiamo disponibilità (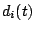 ) e preferenza (
) e preferenza (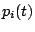 ) dell'utente
) dell'utente 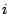 -esimo, dove
-esimo, dove 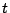 rappresenta il tempo.
rappresenta il tempo.
Definizione 7.2
La funzione di disponibilità 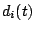 dell'
dell'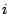 -esimo utente assume i seguenti valori
-esimo utente assume i seguenti valori
La funzione di preferenza 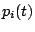 viene costruita a partire dalle preferenze espresse dall'
viene costruita a partire dalle preferenze espresse dall'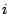 -esimo utente su di una settimana tipo. Esse vengono tradotte in un insieme di valori di preferenza, ovvero valori discreti all'interno di un range predefinito.
-esimo utente su di una settimana tipo. Esse vengono tradotte in un insieme di valori di preferenza, ovvero valori discreti all'interno di un range predefinito.
Definizione 7.3
La funzione di preferenza 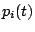 assume il valore di preferenza espresso dall'utente
assume il valore di preferenza espresso dall'utente 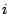 -esimo per il giorno della settimana e l'ora in cui ricade l'istante
-esimo per il giorno della settimana e l'ora in cui ricade l'istante 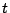 .
.
A partire dalle funzioni di disponibilità e preferenza degli utenti invitati alla riunione, vengono costruite due funzioni obiettivo: la disponibilità media 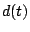 e la preferenza media
e la preferenza media 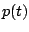 dei partecipanti alla riunione. La disponibilità media
dei partecipanti alla riunione. La disponibilità media 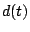 degli utenti invitati è definita nel seguente modo:
degli utenti invitati è definita nel seguente modo:
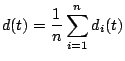 |
(1) |
mentre 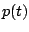 è definita come:
è definita come:
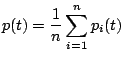 |
(2) |
dove 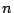 rappresenta il numero di utenti invitati a partecipare alla riunione.
rappresenta il numero di utenti invitati a partecipare alla riunione.
Le possibili soluzioni identificate per soddisfare la richiesta di riunione, costituite da intervalli temporali per la sua collocazione, vengono valutate in base alle funzioni obiettivo che sono state definite. Ad ogni soluzione vengono associati due indici 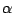 e
e 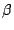 ottenuti integrando le funzioni obiettivo all'interno dell'intervallo da valutare. In particolare, data una soluzione
ottenuti integrando le funzioni obiettivo all'interno dell'intervallo da valutare. In particolare, data una soluzione
![$ \omega = [t_0,t_1]$](img29.png) , si ha
, si ha
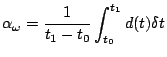 |
(3) |
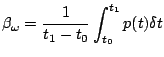 |
(4) |
dove la normalizzazione viene effettuata per rendere confrontabili intervalli di diversa durata.1
Le soluzioni individuate vengono quindi ordinate sulla base degli indici 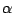 e
e 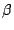 e della loro durata. Il criterio di ordinamento tra due intervalli
e della loro durata. Il criterio di ordinamento tra due intervalli
![$ \omega_1 = [t_0,t_1]$](img33.png) e
e
![$ \omega_2 = [t_2,t_3]$](img34.png) è il seguente:
è il seguente:
dove con 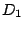 e
e 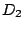 sono state indicate rispettivamente la durata dell'intervallo
sono state indicate rispettivamente la durata dell'intervallo  e quella di
e quella di 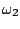 . Si procede confrontando ordinatamente
. Si procede confrontando ordinatamente 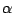 ,
, 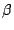 ed infine la durata delle soluzioni in esame. Nel caso in cui questi parametri risultino tutti coincidenti si rispetta l'ordinamento temporale definito dall'istante iniziale di ogni soluzione.
ed infine la durata delle soluzioni in esame. Nel caso in cui questi parametri risultino tutti coincidenti si rispetta l'ordinamento temporale definito dall'istante iniziale di ogni soluzione.
Next: Individuazione delle possibili soluzioni
Up: MMA: gestione delle riunioni
Previous: MMA: gestione delle riunioni
Paolo Toninelli
2006-01-25
![]() invitato alla riunione vengono costruite, sulla base della risposta ricevuta dal suo UPA, due funzioni, che chiamiamo disponibilità (
invitato alla riunione vengono costruite, sulla base della risposta ricevuta dal suo UPA, due funzioni, che chiamiamo disponibilità (![]() ) e preferenza (
) e preferenza (![]() ) dell'utente
) dell'utente ![]() -esimo, dove
-esimo, dove ![]() rappresenta il tempo.
rappresenta il tempo.
![]() e la preferenza media
e la preferenza media ![]() dei partecipanti alla riunione. La disponibilità media
dei partecipanti alla riunione. La disponibilità media ![]() degli utenti invitati è definita nel seguente modo:
degli utenti invitati è definita nel seguente modo:
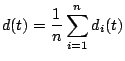
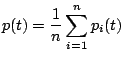
![]() e
e ![]() ottenuti integrando le funzioni obiettivo all'interno dell'intervallo da valutare. In particolare, data una soluzione
ottenuti integrando le funzioni obiettivo all'interno dell'intervallo da valutare. In particolare, data una soluzione
![]() , si ha
, si ha
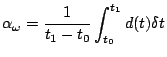
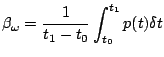
![]() e
e ![]() e della loro durata. Il criterio di ordinamento tra due intervalli
e della loro durata. Il criterio di ordinamento tra due intervalli
![]() e
e
![]() è il seguente:
è il seguente: