
Indici di confronto
tra piani ordinati
con relazioni d'ordine parziale
Lo scopo di questo lavoro consiste nell'individuare alcuni indici in grado di rappresentare le differenze esistenti tra due piani le cui azioni sono vincolate con relazioni d'ordine parziale.
Per chiarezza nell'esposizione saranno utilizzati termini differenti per distinguere le operazioni che compongono il piano. Il termine Azione indicherà d'ora in poi un'operazione in se' e non vincolata all'appartenenza ad un piano. I piani sono composti da Istanze di azioni, in quanto in essi ogni azione puo' apparire piu' volte. Mentre esiste sempre una sola Azione di un certo tipo, in un piano esistono numerose Istanze, alcune delle quali rappresentanti la stessa Azione eseguita piu' volte.

Figura 1: Esempio di piani, istanze ed azioni.
La Figura 1 illustra una situazione tipica. I due piani sono composti da Istanze (rappresentate in minuscolo: a1,b,c,a2, …) che rappresentano Azioni prese da un opportuno insieme predefinito (rappresentate in maiuscolo: A e' l'azione cui appartengono le istanze ai).
Per identificare univocamente un'istanza e' necessario indicarne il piano di appartenenza e numerarle progressivamente: per questo motivo le istanze saranno indicate con il numero di piano ad apice e con il progressivo in pedice; quindi a25 indica la quinta ripetizione nel secondo piano dell'azione A.
All'interno di un piano le istanze sono ordinate da relazioni d'ordine parziale che vincolano temporalmente i tempi di esecuzione delle stesse. Affermeremo che "a12 precede b11" (indicato per brevita' con a12 --> b11) se esiste nel piano 1 una relazione indicante che a12 debba essere eseguita prima di b11. Analogamente esiste la relazione inversa rappresentata da "b12 segue a11" (b12 <-- a11). Due istanze potrebbero non essere in relazione tra loro se l'ordine di esecuzione relativo e' indifferente per l'attuazione del piano; in questo caso la relazione sara' indicata con un tratto (a12 -- b11), indicante che le due istanze possono essere eseguite contemporaneamente oppure indifferentemente prima l'una e poi l'altra.
La Figura 2 illustra le relazioni esistenti nei piani precedentemente rappresentati.
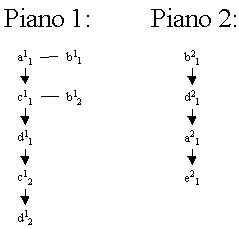
Figura 2: Relazioni tra le istanze dei piani raffigurati in Figura 1.1.
Le relazioni godono della proprieta' di transitivita' per cui se aRb e bRc allora aRc (R indica sia --> che <--). In un piano tutte le coppie di istanze sono tra esse in relazione; tuttavia per chiarezza di rappresentazione le relazioni derivabili per transitivita' non saranno disegnate.
Lo scopo di questo lavoro consiste nel fornire alcuni indici in grado di rappresentare efficacemente ma semplicemente le differenze esistenti tra due piani. Il confronto potrebbe essere molto utile sia nella valutazione di due differenti pianificatori applicati al medesimo problema che nello studio dei piani proposti da un unico pianificatore al variare del problema sottopostogli.
Si considerino i piani della Figura 2. Pur essendo molto simili esistono delle differenze capaci di rendere un piano piu' efficace dell'altro. Avendo a disposizione il piano ottimale e' possibile stabilire quale tra due varianti sia quella migliore confrontandole con esso.
Un primo grossolano confronto puo' essere fatto osservando le Azioni utilizzate da ciascun piano, in quanto se completamente differenti e' probabile che essi si riferiscano a domini diversi.
Molto piu' interessante risulta il confronto delle relazioni, in quanto tramite esse e' possibile analizzare i differenti comportamenti dei pianificatori. Una misura in questo senso e' fornita dalla valutazione del numero di relazioni differenti tra le istanze di un piano e quelle corrispondenti di un altro di riferimento. Per eseguire questo confronto e' necessario associare univocamente tutte le istanze di un piano con quelle dell'altro; puo' quindi essere necessario rimuovere dai piani alcune istanze (quelle che compaiono in un solo piano o piu' numerose).
Un ulteriore valutazione che appare naturale, consiste nel valutare se sia possibile trasformare il secondo piano nel primo semplicemente spostando alcune azioni.
Determinazione degli indici sulle azioni
Il primo confronto puo' essere effettuato ignorando le relazioni tra le istanze ma considerando semplicemente l'insieme di queste che compongono i piani.
Nel caso dell'esempio visto precedentemente e riportato in Figura 3 sono possibili le seguenti considerazioni:
Tutto cio' che si puo' concludere ignorando le relazioni riguarda la presenza di Istanze aggiuntive in un piano rispetto all'altro e l'esistenza di Azioni diverse; pertanto gli indici calcolati riguardano:
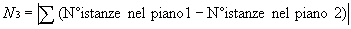

Figura 3: Determinazione degli indici sulle azioni.
Per facilitare la lettura dei risultati e' preferibile normalizzare gli indici calcolati affinche' il loro valore ricada nell'intervallo [0,1] indipendentemente dai piani utilizzati. In particolare, N1 ed N2 possono essere divisi per il numero totale di Azioni presenti complessivamente nei due piani, mentre N3 per il numero totale di Istanze. In questo modo (1-N3') puo' essere usato per esprimere in percentuale quanto i due piani siano simili (a meno delle relazioni); ottenendo per il caso riportato una valore pari al 55%.
Il confronto tra le relazioni tra piani richiede l'associazione in coppie di tutte le istanze del piano di riferimento con le corrispondenti nel secondo piano. In alcune situazioni quest'associazione risulta essere non banale e richiede alcune operazioni preliminari.
La Figura 4 illustra come il problema essenziale da risolvere consiste nello stabilire un metodo per trattare i casi in cui un'istanza non sia associabile o quest'operazione risulti ambigua, come per le istanze cij, bij e dij.
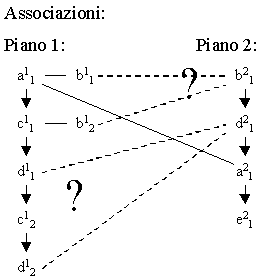
Figura 4: Associazione delle istanze tra i piani.
Una volta associate tutte le istanze per il confronto, e' possibile valutare quante e quali relazioni siano diverse nei due piani.
Rappresentazione delle relazioni
E' possibile rappresentare in forma molto compatta le relazioni presenti in un piano utilizzando una matrice e codificandovi opportunamente le relazioni.
Assumendo che ogni riga ed ogni colonna siano associate univocamente ad un'istanza, l'elemento <i,j> puo' rappresentare la relazione esistente tra l'istanza Ii con Ij. La Figura 5 illustra due piani con le rispettive matrici:
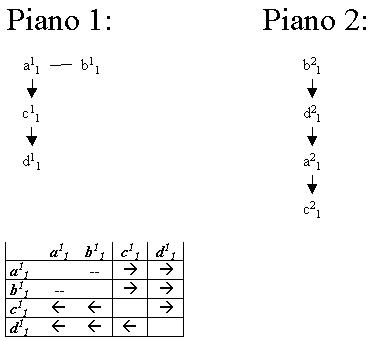
Figura 5: Esempi di piani e rispettive rappresentazioni delle relazioni.
E' necessario osservare che:
E' possibile rappresentare in modo molto compatto la matrice utilizzando un rappresentazione numerica. Numerando le istanze progressivamente con ordine crescente secondo l'ordine con cui appaiono nel piano e rappresentando le relazioni à ,ß ,– e l'identità rispettivamente con +1,-1,0 e 2 si ottiene:
|
a11 |
b11 |
c11 |
d11 |
b21 |
d21 |
a21 |
c21 |
|||
|
a11 |
2 |
0 |
1 |
1 |
b21 |
2 |
1 |
1 |
1 |
|
|
b11 |
0 |
2 |
1 |
1 |
d21 |
-1 |
2 |
1 |
1 |
|
|
c11 |
-1 |
-1 |
2 |
1 |
a21 |
-1 |
-1 |
2 |
1 |
|
|
d11 |
-1 |
-1 |
-1 |
2 |
c21 |
-1 |
-1 |
-1 |
2 |
Figura 6: Rappresentazione matriciale numerica delle relazioni nei piani.
La matrice risulta essere antisimmetrica e pertanto non e' necessaria una rappresentazione completa ma solo parziale (di una triangolare superiore o inferiore).
Se il confronto viene eseguito tra due piani confrontabili (o piani ridotti, generati come illustrato nel seguente paragrafo) le due matrici M1 ed M2 delle relazioni hanno la stessa dimensione e le colonne e righe sono univocamente associate.
E' possibile determinare facilmente le relazioni diverse costruendo una nuova matrice M le cui righe e colonne sono ottenute per differenza tra quelle associate di M1 ed M2. Quest'operazione puo' essere ridotta ad una semplice differenza tra matrici (M=M1-M2) riordinando preventivamente le righe e le colonne di M2 in modo che quelle associate occupino la stessa posizione.
Nella nuova matrice M, tutti gli elementi non nulli rappresentano relazioni differenti tra le medesime coppie di istanze.
La Figura 7 illustra quanto appena affermato.
|
a11 |
b11 |
c11 |
d11 |
a21 |
b21 |
c21 |
d21 |
a1 |
b1 |
c1 |
d1 |
|||||
|
a11 |
2 |
0 |
1 |
1 |
a21 |
2 |
-1 |
1 |
-1 |
a1 |
0 |
1 |
0 |
2 |
||
|
b11 |
0 |
2 |
1 |
1 |
- |
b21 |
1 |
2 |
1 |
1 |
= |
b1 |
-1 |
0 |
0 |
0 |
|
c11 |
-1 |
-1 |
2 |
1 |
c21 |
-1 |
-1 |
2 |
-1 |
c1 |
0 |
0 |
0 |
2 |
||
|
d11 |
-1 |
-1 |
-1 |
2 |
d21 |
1 |
-1 |
1 |
2 |
d1 |
-2 |
0 |
-2 |
0 |
Relazioni non conservate: (a1--b1), (a1à d1), (c1à d1)
Figura 7: Calcolo della matrice differenza.
Si osservi che il numero massimo di relazioni differenti possibile tra due piani e' dato dal numero di elementi contenuti nella triangolare inferiore a meno della diagonale principale. Se la matrice M ha dimensione N, il numero massimo di relazioni risulta essere:
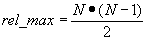
L'indicatore relativo al numero di relazioni differenti puo' quindi essere normalizzato con rel_max per ottenere un indice r' con valore nell'intervallo [0,1].
Per poter confrontare i piani e' necessario associare ogni istanza del piano 1 con una corrispondente istanza del piano 2, rappresentanti entrambe la stessa azione; tuttavia questa operazione non e' univoca in quanto esistono diverse possibilità.
Essendo interessati alla somiglianza tra piani, e' ragionevole richiedere che le associazioni scelte conducano al minor valore possibile per l'indice r, in modo da determinare il massimo valore possibile per l'indice di confronto.
Il problema consiste quindi nell'estrarre dai piani completi originali due sottopiani, caratterizzati dal minor valore di r, in cui tutte le istanze siano associate.
La costruzione puo' essere vista come una ricerca in uno spazio in cui lo stato sia costituito da piani parziali derivabili da quelli iniziali. Ogni stato e' caratterizzato da due piani ridotti, le cui istanze sono reciprocamente ed univocamente associate e da una lista di istanze ancora ambigue (da associare o eliminare). Tale lista assume la forma (<a11, a12; a21 > ; <b11, b12; b21, b22, … , b2n>), elencando tutte le possibili istanze del piano 1 con le possibili istanze associabili del piano 2.
Lo stato iniziale e' costituito dai due sottopiani composti dalle sole istanze banalmente associabili, ossia quelle che appaiono una sola volta in entrambi i piani.
Lo stato finale consiste di due sottopiani in cui tutte le ambiguità siano state risolte ed avente il costo minimo.
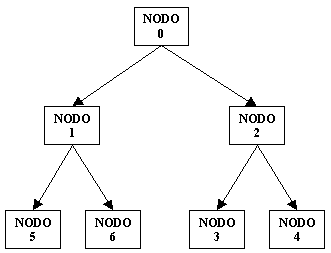
Utilizzando la ricerca A*, che garantisce sotto opportune ipotesi l'esplorazione del minor numero di stati, e' possibile generare un albero di ricerca rappresentante la costruzione progressiva della soluzione (come sarà chiarito in seguito).
Facendo coincidere il nodo iniziale con lo stato iniziale, i successori sono derivati inserendo in entrambi i piani una coppia di istanze selezionate tra quelle ancora ambigue.
All'aumentare della profondità dell'albero, i piani ridotti associati a ciascun nodo aumentano di dimensione (di un'istanza ad ogni livello) e corrispondentemente la lista delle istanze ambigue si riduce. Analogamente, essendo il numero di relazioni strettamente crescente, ad ogni passo il numero di relazioni differenti esistenti tra i due sottopiani risulta monotono crescente, anche se non strettamente; infatti l'inserimento non ha alcun effetto sulle relazioni preesistenti.
Il numero di relazioni differenti risulta essere quindi una buona stima del costo del nodo e garantisce la convergenza della ricerca A* verso la soluzione ottima; inoltre per quanto detto il costo di un nodo e' pari al costo del precedente sommato al numero di relazioni violate dalle sole nuove istanze inserite, in quanto quelle preesistenti sono già state considerate nel calcolo del costo del nodo antenato. Ad ogni passo non e' necessario valutare l'intera matrice delle relazioni, ma solo parte di una sua riga (o colonna).
Essendo la lista delle possibili associazioni finita, il numero degli stati possibili risulta limitato, cosi come la profondità massima dell'albero. Tutti gli obiettivi, ottimali o meno, si trovano ad una ben determinata profondità e pertanto la profondità di un nodo risulta essere inversamente proporzionale alla sua distanza dall'obiettivo.
Per garantire che la ricerca esplori il minor numero di nodi possibile, e' sufficiente espandere a parità di costo i nodi piu' profondi.
Il numero di nodi esplorati puo' essere ulteriormente ridotto eseguendo le scelte piu' vincolanti all'inizio della ricerca, in modo da avere il minor fattore di ramificazione all'inizio. In questo modo, la ricerca A* taglierà porzioni dell'albero piu' numerose.
Raggiunto l'obiettivo, r' deve essere ricalcolato sul piano complessivo al fine di considerare il contributo delle relazioni violate inizialmente nel nodo 0 (quest'operazione potrebbe essere tralasciata inizializzando il costo del nodo 0 al numero effettivo di relazioni violate dai piani ridotti iniziali).
L'esempio finale chiarisce l'algoritmo utilizzato e la generazione dell'albero.
Indice complessivo di confronto
Riassumendo, il confronto tra piani richiede il calcolo di due indici, N3' ed r', indicanti
rispettivamente il numero di istanze differenti ed il numero di relazioni differenti. Mentre il calcolo di N3' e' immediato, la determinazione di r' potrebbe richiedere la generazione di un albero la cui navigazione avviene tramite l'algoritmo di ricerca A*.
La percentuale di istanze presenti in entrambi i piani e quindi associabili per il calcolo di r' e' data da (1-N3'). Un utile indice riassuntivo per la valutazione della somiglianza tra i piani puo' essere ottenuto moltiplicando quest'ultimo valore con il numero di relazioni conservate tra i sottopiani
prescelti per il calcolo di r'.
Tale indice esprime sia il numero di istanze presenti in entrambi i piani che il numero di relazioni tra esse conservate ed e' quindi ottenibile come:
Si supponga di dover confrontare i due piani della Figura 1:

L'algoritmo prevede per prima cosa l'eliminazione delle istanze che appartenenti ad un solo piano: in questo caso c11, c12 ed e21. Ne risultano i due piani seguenti, non ancora confrontabili per via delle istanze multiple:
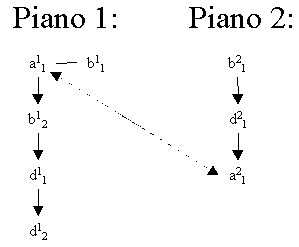
Solamente le due istanze dell'azione A possono essere associate univocamente; pertanto la situazione associata al nodo 0 da cui si dirama l'albero di ricerca sarà:
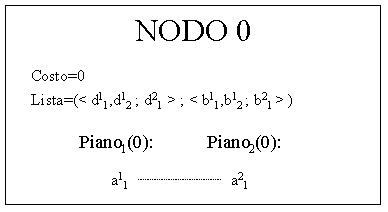
Al passo successivo, la ricerca prevede la generazione di due nodi figli ottenuti inserendo nei piani parziali le azioni D. In questo esempio, poiche' le relative istanze occupano posizioni identiche nei due nodi di primo livello, il costo risulta in entrambi i casi unitario a causa delle differenti relazioni tra le coppie di istanze <d,a>.
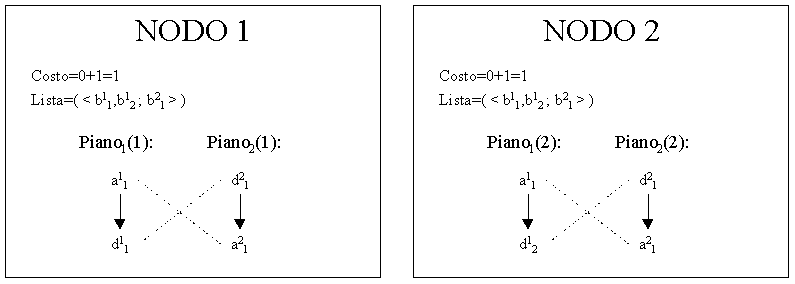
Espandendo ulteriormente il nodo 2 (l'ultimo generato), sono possibili due associazioni alternative per l'istanza b11:
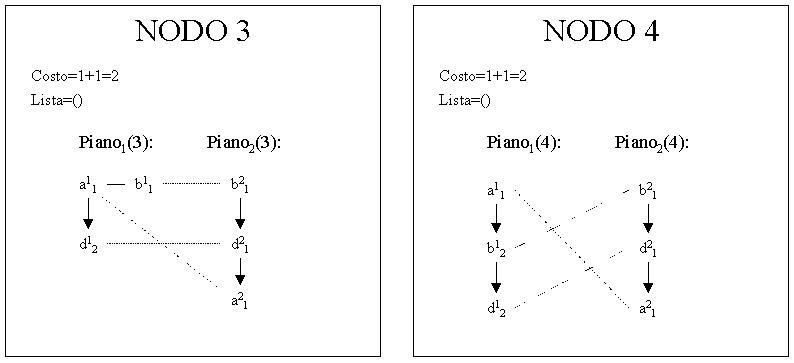
In entrambi i casi, una nuova relazione risulta essere differente tra i due piani parziali incrementando ulteriormente il costo. Avendo effettuato tutte le scelte possibili, la lista delle istanze ambigue risulta vuota e pertanto i nodi 3 e 4 rappresentano due obiettivi; tuttavia essi potrebbero non essere ottimali (col minor costo) in quanto esiste il nodo 1, non ancora espando e con costo inferiore.
In questo esempio, la ricerca A* deve necessariamente espandere tutto l'albero per verificare l'ottimalità degli obiettivi, generando pertanto i nodi:
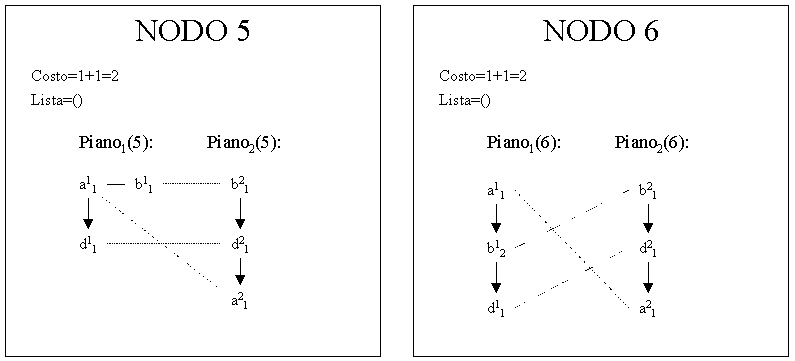
Dati i piani iniziali, sono stati trovati ben 4 obiettivi, tutti equivalenti e caratterizzati dal costo 2. Poiche' il costo di tutti i nodi trascura solamente le relazioni presenti nel nodo iniziale, ed esse si propagano invariate in tutti i nodi successori, il valore effettivo dell'indice r e' pari al costo minimo finale trovato sommato al numero di relazioni differenti esistenti tra i piani del nodo 0, ed e' indipendente dall'obiettivo scelto.
Per quanto riguarda il calcolo di rel_max per la normalizzazione di r, e' necessario considerare che la matrice delle relazioni per i piani parziali degli obiettivi ha dimensione 3x3 (pari al numero di istanze presenti in ciascun piano) e pertanto risulta rel_max=(3*2)/2=3.
Il valore normalizzato degli indici per l'esempio riportato risulta essere:
N3'=5/11=0,45 (il 45% delle istanze e' assente nei piani parziali finali)
r'=2/3=0,67 (il 67% delle relazioni e' diverso tra i piani parziali finali)
Indice complessivo = (1-N3')(1-r') = 0,18
L'indice complessivo puo' variare da 0 (piani completamente diversi) ad 1 (piani uguali). In questo caso, i piani iniziali risultano essere molto diversi.
Un ulteriore indice utile al confronto tra i piani consiste nel numero di azioni che e' necessario spostare per trasformare il secondo piano nel primo.
Considerando che l'ordinamento delle righe e delle colonne delle matrici delle relazioni rispecchia l'ordine delle azioni del piano 1, la matrice differenza ha sempre una struttura particolare.
Si supponga di avere i seguenti piani:
PIANO 1: a à b à c à d
PIANO 2: a à d à b à c
Essi differiscono esclusivamente per la diversa posizione dell'azione d.
Costruendo le matrici delle relazioni e facendone la differenza si ottiene:
| a | b | c | d | |
| a | 0 | 0 | 0 | 0 |
| b | 0 | 0 | 0 | 2 |
| c | 0 | 0 | 0 | 2 |
| d | 0 | -2 | -2 | 0 |
Lo spostamento di un'azione corrisponde sempre all'introduzione di alcuni elementi non nulli sulla sua riga e colonna.
A causa dell'ordine dato alle righe ed alle colonne della matrice, essa risulta antisimmetrica; pertanto tutte le considerazioni possono essere fatte considerando solamente la triangolare inferiore.
Una sequenza di valori negativi su una riga indicano che la relativa istanza nel piano 2 deve essere spostata verso destra (posticipata) rispetto alle istanze corrispondenti agli indici di colonna affinche' siano ripristinate le relazioni esistenti nel piano 1. Viceversa una sequenza di valori negativi lungo una colonna, indicano che la relativa istanza deve essere spostata verso sinistra (anticipata).
Nell'esempio mostrato, analizzando la matrice e' possibile stabilire che i due piani possono essere resi uguali spostando l'azione d, posticipandola dopo b e c.
Supponendo di cambiare anche la posizione dell'azione c, potrebbe accadere che venga ripristinata la corretta relazione tra c e d (cà d). Questo si manifesta nella matrice differenza con l'azzeramento del relativo elemento <d,c> e <c,d>; tuttavia a causa della transitività delle relazioni d'ordine, un altro elemento deve diventare non nullo in quanto si avrebbe: cà d, dà b e quindi dovrebbe essere cà b (c precede b). La nuova relazione violata sarebbe quella tra c e b e la matrice diverrebbe:
| a | b | c | d | |
| a | 0 | 0 | 0 | 0 |
| b | 0 | 0 | 2 | 2 |
| c | 0 | -2 | 0 | 0 |
| d | 0 | -2 | 0 | 0 |
Occorre osservare che mentre la matrice e' stata ottenuta spostando le azioni d e c, dalla rappresentazione si deduce che e' possibile rendere il nuovo piano 2 uguale al primo spostando la sola azione b.
La matrice non dipende da quali manipolazioni siano state eseguite sul piano 2, ma rappresenta lo stato corrente. Teoricamente, si potrebbe assegnare ad ogni configurazione della matrice una descrizione circa le istanze da spostare per trasformare il secondo piano nel primo.
Un metodo piu' ragionevole consiste nell'applicare un algoritmo che analizzando la matrice fornisca la soluzione. L'algoritmo e' il seguente (utilizzando esclusivamente la triangolare inferiore):
La trasformazione del piano 2 nel 1 e' ottenibile spostando le istanze scelte nell'ordine con cui sono state selezionate dall'algoritmo.
Il punto 1 e' necessario per eseguire sempre gli spostamenti che garantiscono il ripristino del maggior numero di relazioni con una sola azione.
Il punto 3 equivale a considerare un piano transitorio parzialmente modificato in cui alcune istanze sono state ricollocate nella sequenza corretta. In realtà, ricalcolando la matrice relativa a tali piani potrebbero esservi ancora elementi non nulli nelle righe o colonne azzerate, tuttavia, l'esistenza del piano di riferimento (il primo) garantisce spostando l'istanza nella posizione finale, al termine dell'algoritmo tutte le relazioni saranno ripristinate e quindi tali elementi verranno annullati. La transitività delle relazioni d'ordine garantisce che vi sia almeno un altro elemento non nullo nella matrice che determinerà lo spostamento dell'altra istanza interessata.
Dato che ad ogni passo vengono ripristinate il maggior numero possibile di relazioni, il numero di istanze spostate e' il minimo possibile e fornisce un'ulteriore stima di quanto differisca il secondo piano dal primo.
Funzionamento del programma "plandiff"
Il programma accetta tre parametri sulla linea di comando, il terzo dei quali e' opzionale. La sintassi e' la seguente:
plandiff <piano1> <piano2> [messaggi]
<piano1> e <piano2> sono rispettivamente i nomi dei file contenenti i piani da confrontare.
[messaggi] e' un numero variabile da 0 a 6 che determina il numero di informazioni visualizzato dal programma durante l'esecuzione. Passandogli il valore 0, il programma visualizzerà solamente la riga dei risultati, stampata in ogni caso alla fine. Essa comprende (nell'ordine riportato e separati da un carattere di tabulazione):
Valori maggiori per messaggi incrementano il numero di informazioni visualizzate secondo il seguente schema:
1) Tabella delle azioni e piani iniziali completi;
2) numero di nodi esplorati con i relativi piani ridotti finali;
4) nodi espansi con i relativi figli e costo;
5) i nodi parziali associati ad ogni nodo espanso;
6) liste delle istanze ambigue rimanenti per ogni nodo espanso.
In allegato la stampa dei messaggi prodotti dal programma confrontando i piani dell'esempio.
La prima operazione compiuta dal programma consiste nella compilazione della tabella delle azioni, con il relativo conteggio e l'associazione ad ogni azione di un codice, assegnato progressivamente man mano le nuove azioni vengono incontrare. Per distinguere le diverse istanze, ognuna di esse viene numerata progressivamente con un secondo indice; pertanto ogni istanza e' individuata univocamente dalla coppia <codice, progressivo>. La tabella delle azioni viene utilizzata per calcolare i primi tre indici.
Per calcolare il numero di relazioni differenti, il programma utilizza una funzione ricerca() che costruisce ricorsivamente l'albero di ricerca secondo quanto esposto in precedenza. E' possibile impostare la ricerca affinche' si arresti al primo obiettivo trovato, prosegua espandendo tutti i nodi con costo non superiore a quello dell'obiettivo oppure espanda tutto l'albero.
Per ulteriori informazioni sul funzionamento del programma si osservino i sorgenti allegati con i relativi commenti.
Esempio dei messaggi mostrati dal programma
Di seguito sono mostrati i messaggi generati dal programma quando eseguito con il parametro relativo impostato al massimo. Il testo e' riconoscibile perche' stampato con un carattere diverso.
All'inizio e' sempre presente un elenco delle azioni trovate, contenente sia il codice assegnato ad ogni azione che il numero delle relative istanze presenti nei piani:.
--------------------------------------------
ELENCO DELLE AZIONI E CONTEGGI:
--------------------------------------------
Codice Cont1 Cont2 Nome dell'azione
0 1 1 a
1 2 1 b
2 2 0 c
3 2 1 d
4 0 1 e
Ne segue la rappresentazione completa dei piani:
--------------------------------------------
PIANI COMPLETI INZIALI:
--------------------------------------------
PIANO <1>
Passo Azione.Progressivo
1: a.1
b.1
2: c.1
b.2
3: d.1
4: c.2
5: d.2
PIANO <2>
Passo Azione.Progressivo
1: b.1
2: d.1
3: a.1
4: e.1
Il passo di esecuzione delle istanze e' sempre un numero intero crescente, con valore iniziale 1. indipendentemente da quanto indicato nei file di ingresso. Le istanze sono individuate univocamente dal codice assegnato all'azione seguito da un progressivo (con valore iniziale 1)assegnato dal programma in fase di caricamento del piano. Ogni riferimento alle istanze avviene in seguito per mezzo di tale codice, per evitare problemi di spazio dovuti ad azioni la cui descrizione risulti eccessivamente lunga.
Poiche' i primi tre indici (N'1,N'2,N'3) possono essere calcolati dalla tabella mostrata all'inizio, essi vengono calcolati immediatamente:
INDICI: 0.200000,0.200000,0.454545
Per calcolare l'indice r' e' necessario procedere con la ricerca euristica al fine di determinare i sottopiani che ne minimizzano il valore. Al fine di mostrare la complessità della ricerca, il contenuto della lista delle possibili scelte viene rappresentato prima della costruzione dell'albero.
La lista Poss elenca tutte le istanze che danno origine alle ambiguità nella valutazione delle relazioni.
INIZIO RICERCA
ELEMENTI DELLA LISTA POSS:
<3.1 3.2 ; 3.1>
<1.1 1.2 ; 1.1>
Ad ogni passo della ricerca viene illustrato il nodo prescelto ed il relativo costo (numero di relazioni violate), seguiti da una rappresentazione dei piani ridotti associati e dall'elenco dei figli.
Per facilitare la comprensione della struttura e della complessità dell'albero, ciascun nodo viene progressivamente numerato man mano che viene generato. Ogni riga dell'elenco contiene tale numero (Figlio), la profondità del nodo (Prof), il costo di tale nodo (Costo) e l'associazione da cui deriva (Assoc). In base a queste informazioni e' possibile costruire una rappresentazione grafica dell'albero e determinare quale sarà il successivo nodo esplorato dal programma.
Opzionalmente, e' possibile visualizzare per ciascun nodo figlio il contenuto della lista Poss, ovviamente identica a quella del genitore ma senza le istanze che compaiono in associate. Quando la lista Poss e' vuota, il nodo rappresenta un potenziale obiettivo, tuttavia esso non verrà riconosciuto come tale finche' la ricerca non lo considererà per l'espansione.
La ricerca puo' essere conclusa al primo obiettivo trovato (condizione di massima efficienza) oppure protratta fino all'espansione di tutti i nodi aventi il costo minimo (onde accertare eventuali errori nel programma) o fino alla generazione dell'intero albero. Nell'esempio riportato si e' scelta la seconda modalità di funzionamento che accerta l'esistenza di 4 obiettivi a costo minimo.
******************************************
NODO 0 (costo 0)
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
Figlio Prof Costo Assoc
1 1 1 <3.1-3.1>
ELEMENTI DELLA LISTA POSS:
<1.1 1.2 ; 1.1>
2 1 1 <3.2-3.1>
ELEMENTI DELLA LISTA POSS:
<1.1 1.2 ; 1.1>
******************************************
NODO 2 (costo 1)
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
5: d .2 -> 2 d .1
Figlio Prof Costo Assoc
3 2 2 <1.1-1.1>
ELEMENTI DELLA LISTA POSS:
4 2 2 <1.2-1.1>
ELEMENTI DELLA LISTA POSS:
******************************************
NODO 1 (costo 1)
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
3: d .1 -> 2 d .1
Figlio Prof Costo Assoc
5 2 2 <1.1-1.1>
ELEMENTI DELLA LISTA POSS:
6 2 2 <1.2-1.1>
ELEMENTI DELLA LISTA POSS:
******************************************
NODO 6 (costo 2)
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
2: b .2 -> 1 b .1
3: d .1 -> 2 d .1
*OBIETTIVO*
******************************************
NODO 5 (costo 2)
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
b .1 -> 1 b .1
3: d .1 -> 2 d .1
*OBIETTIVO*
******************************************
NODO 4 (costo 2)
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
2: b .2 -> 1 b .1
5: d .2 -> 2 d .1
*OBIETTIVO*
******************************************
NODO 3 (costo 2)
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
b .1 -> 1 b .1
5: d .2 -> 2 d .1
*OBIETTIVO*
******************************************
RICERCA TERMINATA: 7 nodi generati
Come passo finale, il programma illustra i piani scelti e le associazioni utilizzate (tramite la ->), riportando poi il calcolo di r,r_max ed r'.
--------------------------------------------
PIANI RIDOTTI SCELTI:
--------------------------------------------
PIANO 1 PIANO 2
Passo Istanza Passo Istanza associata
1: a .1 -> 3 a .1
2: b .2 -> 1 b .1
3: d .1 -> 2 d .1
RELAZIONI VIOLATE: N_rel= 2 N_max=3 (rapp=0.666667)
Una versione semplificata della matrice differenza viene mostrata rappresentando con 0 le relazioni conservate e con 1 quelle violate.
MATRICE:
0 1 1
1 0 0
1 0 0
Dalla matrice vengono determinate le istanze fuori posto, mostrando la direzione in cui dovrebbero essere spostate nel piano 2 affinche' i piani ridotti diventino uguali (<-/-> indica che l'istanza deve essere anticipata/posticipata rispetto alla posizione corrente).
SPOSTAMENTI:
a.1 <--
ISTANZE DA SPOSTARE=1
Infine viene riportata la riga riassuntiva dei risultati, l'unica visibile qualora si utilizzi il valore 0 (default) per il parametro dei messaggi:
es1a.plan es1b.plan 0.200000 0.200000 0.454545 2 3 0.666667 1 0.181818
Il programma e' stato sviluppato come strumento di confronto tra piani, ma in realtà esso si inserisce in un progetto piu' ampio nel quale costituisce solamente uno strumento di verifica e valutazione.
Il progetto prevede lo sviluppo di tecniche per la pianificazione capaci di risolvere delle varianti di problemi standard (noti in letteratura) tramite l'adattamento della soluzione del caso generale. Tali problemi sono generalmente utilizzati per la verifica dei pianificatori e nella formulazione tradizionale la soluzione ottima (nel senso della minimizzazione del numero di passi richiesti dal piano) e' nota.
I pianificatori sviluppati nell'ambito del progetto di ricerca consentono la determinazione di possibili soluzioni a problemi derivati da quelli standard modificandone gli obiettivi o le condizioni iniziali. Ulteriore requisito richiesto alla soluzione determinata e' che il piano adattato sia "simile" a quello standard.
Il programma sviluppato durante questo lavoro costituisce uno strumento per il confronto e la valutazione dei piani generati, rendendo possibile un confronto tra le diverse tecniche previste.
In seguito sono illustrati i risultati ottenuti da alcuni dei problemi standard, in particolare per i due domini Rocket e Logistic.
In Rocket il problema consiste nel portare a destinazione determinati oggetti, inizialmente posti in alcuni luoghi, utilizzando opportuni vettori.
In Logistic, oggetti o persone devono essere portate a destinazione utilizzando aeroplani e autotrasporti, prevedendo quindi un'interazione piu' complessa avendo due mezzi di trasporto differenti a disposizione.
Per entrambi i domini esistono diversi problemi standard, indicati con: Rocket A, Rocket B; Logistic A, Logistic B e Logistic C.
Ogni problema e' stato modificato, risolto con tre tecniche diverse e la soluzione confrontata con quella ottima del piano del problema originale.
Le tre tecniche adottate sono: pianificazione tramite Planning Graph (IPP, produce una soluzione ottima), ricerca sistematica (SIST) e ricerca locale-sistematica (LOC-SIS).
Per fornire uno strumento valido e rapido per la valutazione dei numerosi dati prodotti, sono state create delle procedure automatiche per la realizzazione di grafici contenenti gli indici ottenuti. La lettura dei grafici risulta decisamente piu' chiara ordinando i dati secondo un ordine decrescente dell'indice prodotto dalla tecnica IPP.
Dai grafici si puo' rilevare come le tecniche di ricerca LOC-SIS e SIST, sviluppate durante la ricerca, producano dei piani con un indice di somiglianza r' che si mantiene sempre su valori elevati, indicando che la soluzione non differisce molto dal piano standard. Al contrario, il valore raggiunto dalle soluzioni proposte da IPP raggiunge livelli notevolmente inferiori, indicando che i piani sono stati per la maggior parte ricostruiti.
Per molti problemi, si verifica inoltre l'incapacità di IPP di fornire una soluzione utilizzando le risorse di calcolo e temporali assegnate, mentre le tecniche alternative sono in grado di determinare dei piani accettabili.
Conclusioni e possibili sviluppi
Il progetto ha condotto alla costruzione di uno strumento di confronto tra piani utile per la valutazione di tecniche di pianificazione, in particolare la rappresentazione grafica dei risultati consente una rapida e sintetica valutazione della grande mole di dati prodotta dai test.
Nel corso del progetto, un'analisi critica dei grafici ha condotto all'individuazione di alcuni errori nel codice dei pianificatori, consentendone la rimozione.
Al fine di migliorare la valutazione, ulteriori approfondimenti dovrebbero essere rivolti alla determinazione del minor numero di azioni da spostare (indice di spostamento). In particolare, potrebbe essere utile modificare la funzione costo della ricerca euristica al fine di minimizzare l'indice di spostamento, determinando in tal modo i piani ridotti caratterizzati dalla possibilità di trasformazione dell'uno nell'altro spostando il minor numero di istanze.
Attualmente, il confronto avviene attribuendo a ciascuno dei due indici parziali r' ed N'3 lo stesso peso. Potrebbe essere interessante analizzare i risultati introducendo dei coefficienti correttivi in grado di modificare il peso dei due indici. In particolare, definendo l'indice complessivo come:
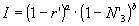
bisognerebbe valutare l'effetto degli esponenti a e b per individuare i criteri di valutazione ottimali.