Torna alla Home Page del corso    Torna alla pagina degli Elaborati

BACKTRACKING CRONOLOGICO E BACKJUMPING: L’ESEMPIO DELLE N-REGINE.
Ma come funziona il backtracking? Vediamo con una semplice animazione il funzionamento di due tipi di backtracking, il backtracking cronologico e il backjumping, nel problema della n-regine formulato in CSP. In ogni frame dell’animazione seguente a sinistra è visualizzata la scacchiera, mentre a destra è visualizzato il corrispondente albero di ricerca. Si noti che sulla scacchiera ogni posizione vietata è rappresentata da una casella grigia, nella quale è indicato il numero della colonna la cui regina vieta proprio la posizione in questione; invece nell’albero di ricerca i nodi grigi sono i nodi visitati ma che non possono essere accettati perché violerebbero qualche vincolo.

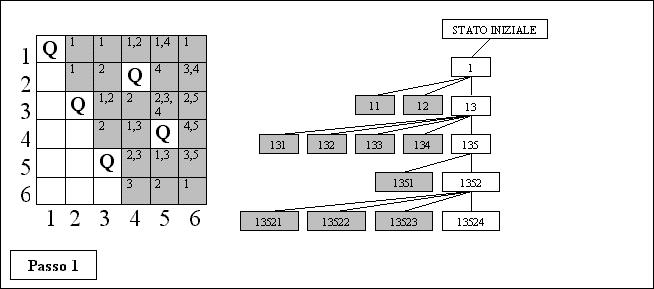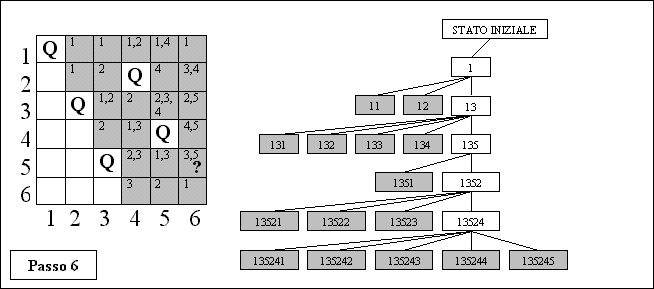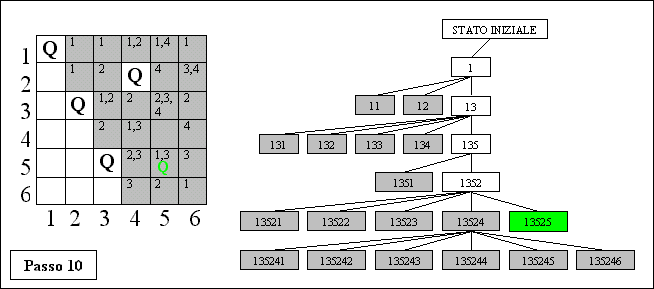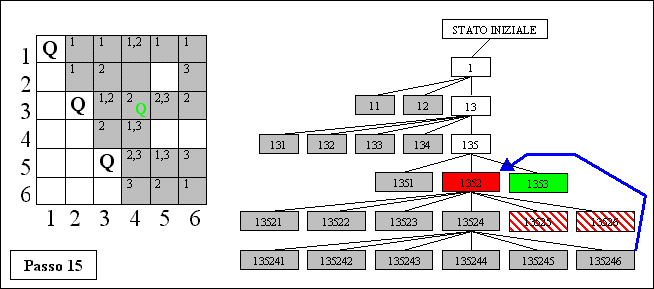
Passo 1: Si supponga che con la ricerca si sia giunti alla tupla (1,3,5,2,4), che chiaramente può essere accettata perché nessuna regina è attaccata da altre.
Passo 2: L’algoritmo di ricerca prova a posizionare l’ultima regina (quella della colonna 6) sulla riga 1, ma verrebbe attaccata dalla regina della colonna 1…
Passo 3: sulla riga 2, ma verrebbe attaccata dalle regine delle colonne 3 e 4…
Passo 4: sulla riga 3, ma verrebbe attaccata dalle regine delle colonne 2 e 5…
Passo 5: sulla riga 4, ma verrebbe attaccata dalle regine delle colonne 4 e 5…
Passo 6: sulla riga 5, ma verrebbe attaccata dalle regine delle colonne 3 e 5…
Passo 7: sulla riga 6, ma verrebbe attaccata dalla regina della colonne 1.
Passo 8: Si è quindi giunti ad un vicolo cieco, poiché non è possibile trovare una soluzione con la regina della colonna 5 sulla riga 4: è necessario fare un passo indietro e provare con una nuova istanziazione.
Passo 9: L’algoritmo deve quindi tornare al livello precedente…
Passo 10: … e provare a spostare la regina della colonna 5 sulla riga 5. Ma in questa posizione la regina verrebbe attaccata dalle regine delle colonne 1 e 3.
Passo 11: Pertanto si sposta la regina dalla colonna 5 sulla riga 6. Ma in questa posizione verrebbe attaccata dalla regina della colonna 2.
Passo 12: Ancora una volta si è giunti ad un vicolo cieco, in quanto non è possibile trovare una soluzione con la regina della colonna 4 sulla riga 2.
Passo 13: Sarà necessario tornare al livello precedente…
Passo 14: … e provare a spostare la regina della colonna 4 sulla riga 3. E così via.

Nei Passi 9-10 e 13-14 è stato applicato il BACKTRACKING CRONOLOGICO: quando si verifica un vicolo cieco (Passi 8-12) significa che non è possibile trovare nessunaposizione valida per la regina che si sta considerando, poiché in ogni possibile riga è attaccata da almeno una delle regine precedenti. Quindi si torna al livello precedente (Passi 9-13) e si sposta la relativa regina in una nuova posizione (Passi 10-14), nella speranza che la nuova configurazione possa rendere possibile una soluzione.
MA IN QUESTO ESEMPIO, TUTTI I PASSI EFFETTUATI ERANO PROPRIO NECESSARI? Se si osserva la scacchiera al Passo 8 si può notare facilmente che spostare la regina della colonna 5 (Passo 10) non serve a nulla, in quanto tutte le posizioni della colonna 6 rimarrebbero in ogni caso vietate perché attaccate da regine precedenti. Pertanto si può pensare ad un algoritmo più efficiente, che salti i Passi 9-10-11-12-13 ed effettui direttamente il Passo 15: in questo modo l’algoritmo non visita i nodi tratteggiati in rosso, e risulta quindi più efficiente. E questo è il BACKJUMPING.

PASSO 15: Quando si verifica un vicolo cieco è possibile evitare di tornare al livello immediatamente precedente: si può fare un "salto" più lungo e ritornare al livello del nodo che è la vera causa del vicolo cieco.

Nel nostro elaborato ci siamo poi occupati anche di altri tre tipi di backtracking (conflict-directed backtracking, forward checking e backmarking): oltre alla loro definizione è stato possibile ottenere una gerarchia che stabilisce quali sono i più efficienti e verificare la gerarchia con prove sperimentali.
 

Precedente    Successiva